単一ソースの最短経路、任意の重み

単一ソース最短経路アルゴリズム（任意の重みが正または負の場合）も知られています。ベルマンフォードアルゴリズムは、ソース頂点から他の頂点までの最小距離を見つけるために使用されます。このアルゴリズムとダイクストラのアルゴリズムの主な違いは、ダイクストラのアルゴリズムでは負の重みを処理できないことですが、ここでは簡単に処理できます。

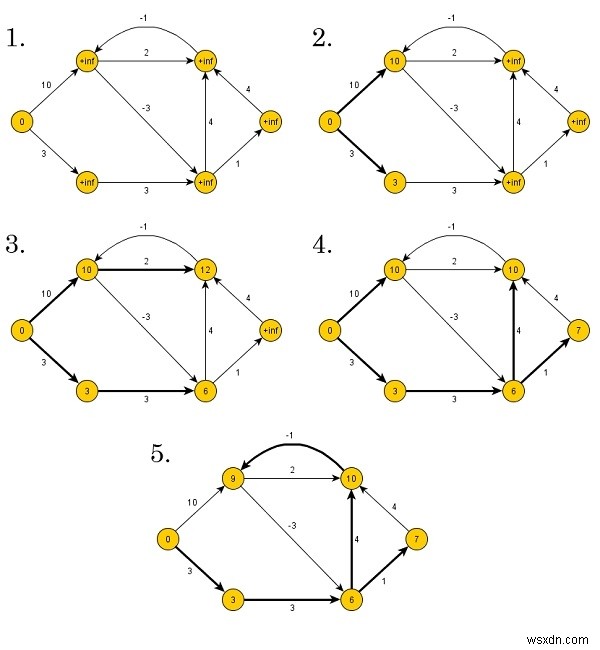
Bellman-Fordアルゴリズムは、ボトムアップ方式で距離を検出します。最初に、パスにエッジが1つしかない距離を見つけます。その後、パスの長さを増やして、考えられるすべての解決策を見つけます。

入力 −グラフのコストマトリックス：

0 6 ∞ 7 ∞
∞ 0 5 8 -4
∞ -2 0 ∞ ∞
∞ ∞ -3 0 9
2 ∞ 7 ∞ 0

出力 −ソース頂点：2
頂点：0 1 2 3 4
距離：-4 -2 0 3 -6
Pred：4 2 -1 0 1
グラフには負のエッジサイクルはありません

アルゴリズム

bellmanFord（dist、pred、source）

入力 −距離リスト、先行リスト、およびソース頂点。

出力 −真、負のサイクルが見つかった場合。

Begin
   iCount := 1
   maxEdge := n * (n - 1) / 2 //n is number of vertices
   for all vertices v of the graph, do
      dist[v] := ∞
      pred[v] := ϕ
   done
   dist[source] := 0
   eCount := number of edges present in the graph
   create edge list named edgeList
   while iCount < n, do
   for i := 0 to eCount, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i)
         dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i)
         pred[edgeList[i].v] := edgeList[i].u
      done
   done
   iCount := iCount + 1
   for all vertices i in the graph, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i), then
         return true
      done
   return false
End

例（C ++）

#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//Cost matrix of the graph (directed) vertex 5
int costMat[V][V] = {
   {0, 6, INF, 7, INF},
   {INF, 0, 5, 8, -4},
   {INF, -2, 0, INF, INF},
   {INF, INF, -3, 0, 9},
   {2, INF, 7, INF, 0}
};
typedef struct{
   int u, v, cost;
}edge;
int isDiagraph(){
   //check the graph is directed graph or not
   int i, j;
   for(i = 0; i<V; i++){
      for(j = 0; j<V; j++){
         if(costMat[i][j] != costMat[j][i]){
            return 1;//graph is directed
         }
      }
   }
   return 0;//graph is undirected
}
int makeEdgeList(edge *eList){
   //create edgelist from the edges of graph
   int count = -1;
   if(isDiagraph()){
      for(int i = 0; i<V; i++){
         for(int j = 0; j<V; j++){
            if(costMat[i][j] != 0 && costMat[i][j] != INF){
               count++;//edge find when graph is directed
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }else{
      for(int i = 0; i<V; i++){
         for(int j = 0; j<i; j++){
            if(costMat[i][j] != INF){
               count++;//edge find when graph is undirected
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }
   return count+1;
}
int bellmanFord(int *dist, int *pred,int src){
   int icount = 1, ecount, max = V*(V-1)/2;
   edge edgeList[max];
   for(int i = 0; i<V; i++){
      dist[i] = INF;//initialize with infinity
      pred[i] = -1;//no predecessor found.
   }
   dist[src] = 0;//for starting vertex, distance is 0
   ecount = makeEdgeList(edgeList); //edgeList formation
   while(icount < V){ //number of iteration is (Vertex - 1)
      for(int i = 0; i<ecount; i++){
         if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]){
            //relax edge and set predecessor
            dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
            pred[edgeList[i].v] = edgeList[i].u;
         }
      }
      icount++;
   }
   //test for negative cycle
   for(int i = 0; i<ecount; i++){
      if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]){
         return 1;//indicates the graph has negative cycle
      }
   }
   return 0;//no negative cycle
}
void display(int *dist, int *pred){
   cout << "Vert: ";
   for(int i = 0; i<V; i++)
      cout <<setw(3) << i << " ";
   cout << endl;
   cout << "Dist: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << dist[i] << " ";
   cout << endl;
   cout << "Pred: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << pred[i] << " ";
   cout << endl;
}
int main(){
   int dist[V], pred[V], source, report;
   source = 2;
   report = bellmanFord(dist, pred, source);
   cout << "Source Vertex: " << source<<endl;
   display(dist, pred);
   if(report)
      cout << "The graph has a negative edge cycle" << endl;
   else
      cout << "The graph has no negative edge cycle" << endl;
}

出力

Source Vertex: 2
Vert: 0 1 2 3 4
Dist: -4 -2 0 3 -6
Pred: 4 2 -1 0 1
The graph has no negative edge cycle