単一ソースの最短経路、非負の重み

単一ソースの最短経路アルゴリズム（非負の重みの場合）は、ダイクストラアルゴリズムとも呼ばれます。隣接行列表現を持つ特定のグラフG（V、E）があり、ソース頂点も提供されます。ソース頂点からグラフGの他の頂点までの最短最短経路を見つけるダイクストラのアルゴリズム。

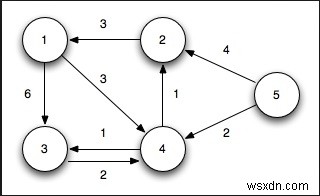
開始ノードから他のノードまで、最小距離を見つけます。この問題では、グラフは隣接行列を使用して表されます。 （この目的では、コストマトリックスと隣接マトリックスは類似しています。）

入力 −隣接行列-

0 3 6 ∞ ∞ ∞ ∞
3 0 2 1 ∞ ∞ ∞
6 2 0 1 4 2 ∞
∞ 1 1 0 2 ∞ 4
∞ ∞ 4 2 0 2 1
∞ ∞ 2 ∞ 2 0 1
∞ ∞ ∞ 4 1 1 0

出力 −

0 to 1, Using: 0, Cost: 3

0 to 2, Using: 1, Cost: 5

0 to 3, Using: 1, Cost: 4

0 to 4, Using: 3, Cost: 6

0 to 5, Using: 2, Cost: 7

0 to 6, Using: 4, Cost: 7

アルゴリズム

dijkstraShortestPath（n、dist、next、start）

入力 −ノードの総数n、各頂点の距離リスト、次に来るノードを格納する次のリスト、およびシードまたは開始頂点。​​

出力 −開始から他のすべての頂点までの最短経路。

Begin
   create a status list to hold the current status of the selected node
   for all vertices u in V do
      status[u] := unconsidered
      dist[u] := distance from source using cost matrix
      next[u] := start
   done
   status[start] := considered, dist[start] := 0 and next[start] := φ
   while take unconsidered vertex u as distance is minimum do
      status[u] := considered
      for all vertex v in V do
         if status[v] = unconsidered then
         if dist[v] > dist[u] + cost[u,v] then
            dist[v] := dist[u] + cost[u,v]
            next[v] := u
      done
   done
End

例（C ++）

#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
   {0, 3, 6, INF, INF, INF, INF},
   {3, 0, 2, 1, INF, INF, INF},
   {6, 2, 0, 1, 4, 2, INF},
   {INF, 1, 1, 0, 2, INF, 4},
   {INF, INF, 4, 2, 0, 2, 1},
   {INF, INF, 2, INF, 2, 0, 1},
   {INF, INF, INF, 4, 1, 1, 0}
};
int minimum(int *status, int *dis, int n){
   int i, min, index;
   min = INF;
   for(i = 0; i<n; i++)
      if(dis[i] < min && status[i] == 1){
      min = dis[i];
      index = i;
   }
   if(status[index] == 1)
      return index;//minimum unconsidered vertex distance
   else
      return -1;//when all vertices considered
}
void dijkstra(int n, int *dist,int *next, int s){
   int status[V];
   int u, v;
   //initialization
   for(u = 0; u<n; u++){
      status[u] = 1;//unconsidered vertex
      dist[u] = costMat[u][s];//distance from source
      next[u] = s;
   }
   //for source vertex
   status[s] = 2; dist[s] = 0; next[s] = -1;//-1 for starting vertex
   while((u = minimum(status, dist, n)) > -1){
      status[u] = 2;//now considered
      for(v = 0; v<n; v++)
         if(status[v] == 1)
            if(dist[v] > dist[u] + costMat[u][v]){
      dist[v] = dist[u] + costMat[u][v];//update distance
      next[v] = u;
      }
   }
}
main(){
   int dis[V], next[V], i, start = 0;
   dijkstra(V, dis, next, start);
   for(i = 0; i<V; i++)
      if(i != start)
         cout << start << " to " << i <<", Using: " << next[i] << ", Cost: " << dis[i] << endl;
}

出力

0 to 1, Using: 0, Cost: 3

0 to 2, Using: 1, Cost: 5

0 to 3, Using: 1, Cost: 4

0 to 4, Using: 3, Cost: 6

0 to 5, Using: 2, Cost: 7

0 to 6, Using: 4, Cost: 7