正確にk個のエッジを持つ最短経路

1つの有向グラフには、頂点の各ペア間の重みが示され、2つの頂点uとvも提供されます。私たちのタスクは、頂点uから頂点vまでの最短距離を、正確にk個のエッジで見つけることです。

この問題を解決するために、頂点uから開始し、隣接するすべての頂点に移動し、k値をk-1として使用して隣接する頂点に対して繰り返します。

入力と出力

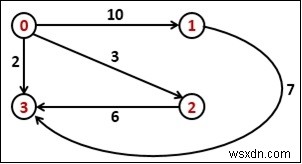
Input:
The cost matrix of the graph.
0 10 3 2
∞  0 ∞ 7
∞  ∞ 0 6
∞  ∞ ∞ 0

Output:
Weight of the shortest path is 9

アルゴリズム

shortKEdgePath(u, v, edge)

入力- 頂点uとv、およびいくつかのエッジ。

出力- 最短経路の距離。

Begin
   if edge = 0 and u = v, then
      return 0
   if edge = 1 and cost[u, v] ≠ ∞, then
      return cost[u, v]
   if edge <= 0, then
      return ∞
   set shortPath := ∞

   for all vertices i, do
      if cost[u, i] ≠ ∞ and u ≠ i and v ≠ i, then
         tempRes := shortKEdgePath(i, v, edge - 1)
         if tempRes ≠ ∞, then
            shortPath = minimum of shortPath and (cost[u,i]+tempRes
   done
   return shortPath
End

例

#include <iostream>
#define NODE 4
#define INF INT_MAX
using namespace std;

int cost[NODE][NODE] = {
   {0, 10, 3, 2},
   {INF, 0, INF, 7},
   {INF, INF, 0, 6},
   {INF, INF, INF, 0}
};

int minimum(int a, int b) {
   return (a<b)?a:b;
}

int shortKEdgePath(int u, int v, int edge) {
   if (edge == 0 && u == v)    //when 0 edge, no path is present            
      return 0;
   if (edge == 1 && cost[u][v] != INF)    //when only one edge, and (u,v) is valid
      return cost[u][v];
   if (edge <= 0)    //when edge is -ve, there are infinity solution        
      return INF;
   int shortPath = INF;

   for (int i = 0; i < NODE; i++) {    //for all vertices i, adjacent to u
      if (cost[u][i] != INF && u != i && v != i) {
         int tempRes = shortKEdgePath(i, v, edge-1);
         if (tempRes != INF)
            shortPath = minimum(shortPath, cost[u][i] + tempRes);
      }
   }
   return shortPath;
}

int main() {
   int src = 0, dest = 3, k = 2;
   cout << "Weight of the shortest path is " << shortKEdgePath(src, dest, k);
}

出力

Weight of the shortest path is 9