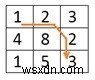
最小コストパス

マトリックスの各セルは、そのセルを通過するためのコストを表します。

セルからはどこにも移動できません。目的地に到達するために、右または下、または右下の対角セルに移動できます。

入力と出力

Input:
The cost matrix. And the destination point. In this case the destination point is (2, 2).
1 2 3
4 8 2
1 5 3

Output:
The minimum cost to reach to the destination from (0, 0). The minimum cost is 8.

アルゴリズム

minCostPath(destX, destY, cost)

入力- 目的地の（x、y）の場所、およびコストマトリックス。

出力- 目的地に到達するための最小コスト。

Begin
   define matrix totalCost, whose order is same as cost matrix
   totalCost[0, 0] = cost[0, 0]

   for i := 1 to destX, do
      totalCost[i, 0] := totalCost[i-1, 0] + cost[i, 0]
   done

   for j := 1 to destY, do
      totalCost[0, j] := totalCost[0, j-1] + cost[0, j]
   done

   for all places (i, j) from (1, 1) to (destX, destY), do
      totalCost[i, j] := minimum of totalCost[i-1, j-1], totalCost[i-1, j] and (totalCost[i, j-1] + cost[i,j])
   done

   return totalCost[destX, destY]
End

例

#include<iostream>
#define ROW 3
#define COL 3
using namespace std;

int cost[ROW][COL] = {
   {1, 2, 3},
   {4, 8, 2},
   {1, 5, 3}
};

int min(int a, int b, int c) {
   return (a<b)?((a<c)?a:c):((b<c)?b:c);
}

int minCostPath(int destX, int destY) {
   int totalCost[ROW][COL];

   totalCost[0][0] = cost[0][0];

   for (int i = 1; i <= destX; i++)
      totalCost[i][0] = totalCost[i-1][0] + cost[i][0];    //set first col of totalCost array

   for (int j = 1; j <= destY; j++)            //set first row of totalCost array
      totalCost[0][j] = totalCost[0][j-1] + cost[0][j];

   for (int i = 1; i <= destX; i++)            //for second row and column to all
      for (int j = 1; j <= destY; j++)
         totalCost[i][j] = min(totalCost[i-1][j-1], totalCost[i- 1][j], totalCost[i][j-1]) + cost[i][j];
   return totalCost[destX][destY];
}

int main() {
   cout << "Minimum Cost: "<< minCostPath(2, 2);    //destination (2, 2)
   return 0;
}

出力

Minimum Cost: 8