強く接続されたグラフ

有向グラフでは、1つのコンポーネントの頂点の各ペアの間にパスがある場合、強く接続されていると言われます。

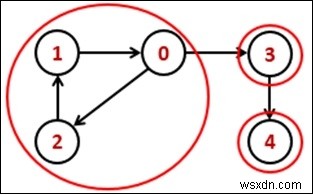
このアルゴリズムを解決するには、まず、DFSアルゴリズムを使用して各頂点の終了時間を取得し、次に転置されたグラフの終了時間を検索します。次に、頂点をトポロジカルソートの降順で並べ替えます。

入力と出力

Input:
Adjacency matrix of the graph.
0 0 1 1 0
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
0 0 0 0 0

Output:
Following are strongly connected components in given graph:
0 1 2
3
4

アルゴリズム

トラバース（グラフ、開始、訪問済み）

入力： トラバースされるグラフ、開始頂点、および訪問したノードのフラグ。

出力： DFS手法の各ノードを通過し、ノードを表示します。

Begin
   mark start as visited
   for all vertices v connected with start, do
      if v is not visited, then
         traverse(graph, v, visited)
   done
End

topoSort（u、visited、stack）

入力- 開始ノード、訪問した頂点のフラグ、スタック。

出力- グラフを並べ替えながらスタックを埋めます。

Begin
   mark u as visited
   for all node v, connected with u, do
      if v is not visited, then
         topoSort(v, visited, stack)
   done
   push u into the stack
End

getStrongConComponents（graph）

入力： 与えられたグラフ。

出力- 強く接続されたすべてのコンポーネント。

Begin
   initially all nodes are unvisited
   for all vertex i in the graph, do
      if i is not visited, then
         topoSort(i, vis, stack)
   done

   make all nodes unvisited again
   transGraph := transpose of given graph

   while stack is not empty, do
      pop node from stack and take into v
      if v is not visited, then
         traverse(transGraph, v, visited)
   done
End

例

#include <iostream>
#include <stack>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 0, 1, 1, 0},
   {1, 0, 0, 0, 0},
   {0, 1, 0, 0, 0},
   {0, 0, 0, 0, 1},
   {0, 0, 0, 0, 0}
};
                               
int transGraph[NODE][NODE];

void transpose() {    //transpose the graph and store to transGraph
   for(int i = 0; i<NODE; i++)
      for(int j = 0; j<NODE; j++)
         transGraph[i][j] = graph[j][i];
}    
         
void traverse(int g[NODE][NODE], int u, bool visited[]) {
   visited[u] = true;    //mark v as visited
   cout << u << " ";

   for(int v = 0; v<NODE; v++) {
      if(g[u][v]) {
         if(!visited[v])
            traverse(g, v, visited);
      }
   }
}  
                                               
void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;    //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {    //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }

   stk.push(u);    //push starting vertex into the stack
}

void getStrongConComponents() {
   stack<int> stk;
   bool vis[NODE];

   for(int i = 0; i<NODE; i++)
      vis[i] = false;    //initially all nodes are unvisited
   
   for(int i = 0; i<NODE; i++)
      if(!vis[i])    //when node is not visited
         topoSort(i, vis, stk);
   
   for(int i = 0; i<NODE; i++)
      vis[i] = false;    //make all nodes are unvisited for traversal  
   transpose();    //make reversed graph
   
   while(!stk.empty()) {    //when stack contains element, process in topological order
      int v = stk.top(); stk.pop();
      if(!vis[v]) {
         traverse(transGraph, v, vis);
         cout << endl;
      }
   }
}

int main() {
   cout << "Following are strongly connected components in given graph: "<<endl;
   getStrongConComponents();
}

出力

Following are strongly connected components in given graph:
0 1 2
3
4