データ構造内のトーナメントツリー、勝者ツリー、敗者ツリー
ここでは、トーナメントツリー、勝者ツリー、ルーザーツリーが表示されます。トーナメントツリーは、n個の外部ノードとn –1個の内部ノードを持つ完全なバイナリツリーです。外部ノードはプレーヤーを表し、内部ノードは2人のプレーヤー間の試合の勝者を表します。このツリーは、選択ツリーとも呼ばれます。
トーナメントツリーにはいくつかのプロパティがあります。これらは以下のようなものです-
-
この木は根付いています。したがって、ツリー内のリンクと親から子への方向付けられたパス、および親のない一意の要素があります
-
親の値は、一般的な比較演算子のノード以下であり、親と子の相対値がツリー全体で不変である限り使用できます
-
2の累乗ではないノードの数を持つツリーには、穴が含まれています。穴はツリーのどこにでも存在できます。
-
このツリーは、バイナリヒープの適切な一般化です
-
ルートはトーナメントの総合優勝者を表します。
トーナメントツリーには2つのタイプがあります-
-
勝者ツリー
-
ルーザーツリー
勝者ツリー
勝者ツリーは完全な二分木であり、各ノードは2つの子のうち小さい方または大きい方を表し、勝者ツリーと呼ばれます。ルートは、ツリーの最小または最大のノードを保持しています。トーナメントツリーの勝者は、すべてのシーケンスの中で最小または最大のnキーです。勝者ツリーがO(log n)時間で形成されることは簡単にわかります。
例 − 3、5、6、7、20、8、2、9のキーがあるとします
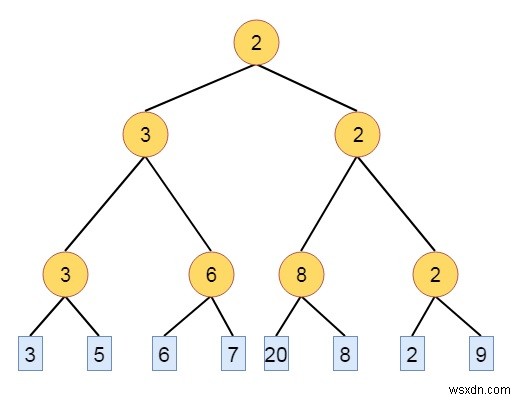
ルーザーツリー
ルーザーツリーは、n個の外部ノードとn –1個の内部ノードが存在するn人のプレーヤーのための完全なバイナリツリーです。一致の緩いものは内部ノードに保存されます。しかし、この全体的な勝者はtree[0]に保存されます。緩いものは代替表現であり、対応するノードでの一致の緩いものを格納します。より緩いの利点は、勝者ツリーが出力された後にツリーを再構築するには、このパス上のノードの兄弟ではなく、リーフからルートへのパス上のノードを調べるだけで十分なことです。
例 −より緩いツリーを形成するには、最初に勝者ツリーを作成する必要があります。
10、2、7、6、5、9、12、1のキーがあるとします。そのため、最初に最小の勝者ツリーを作成します。
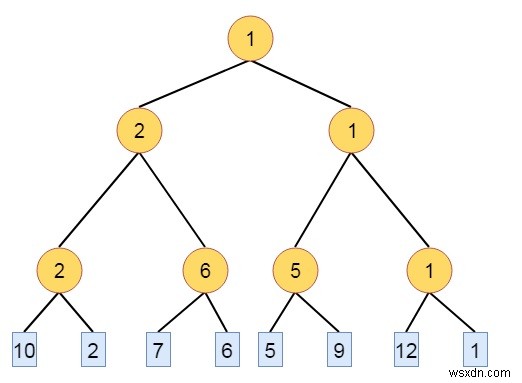
ここで、より緩い一致を各内部ノードに保存します。
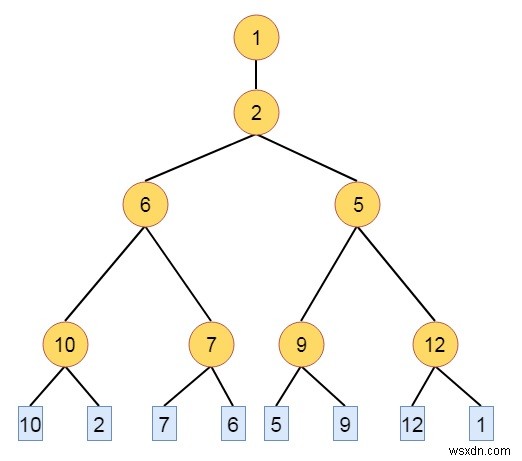
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
-
データ構造の二分木とプロパティ
このセクションでは、1つの二分木データ構造のいくつかの重要なプロパティを確認します。このような二分木があるとします。 一部のプロパティは-です レベル「l」のノードの最大数は$2^{l-1}$になります。ここで、レベルは、ルート自体を含む、ルートからノードへのパス上のノードの数です。ルートのレベルは1であると考えています。 高さhの二分木に存在するノードの最大数は$2^ {h}-1$です。ここで、heightは、ルートからリーフへのパス上のノードの最大数です。ここでは、1つのノードを持つ木の高さが1であると考えています。 n個のノードを持つ二分木では、可能な最小の高さまたは最小のレ
