データ構造入門：ハフマン木（ハフマンツリー）の基礎と符号化の仕組み
ハフマン木とは？定義
ハフマン符号化（Huffman coding）は、各文字に出現頻度（重み）に応じた長さの符号を割り当てる圧縮手法です。ハフマン符号は可変長であり、かつ接頭辞条件（どの符号も他の符号の先頭部分にならない性質）を満たします。このような接頭辞条件を満たす2進符号は、符号化された文字を葉に配置した二分木として表現できます。
ハフマン木（ハフマン符号木）とは、木のすべての葉が与えられたアルファベットの各文字に対応する完全二分木として定義されます。
また、ハフマン木は「外部経路重みが最小」となる二分木として捉えられます。これは、与えられた葉の集合に対して、重み付き経路長の総和が最小になる木ということです。したがって、ハフマン木構築の目的は、外部経路重みを最小化する木を作ることにあります。
以下に具体的な例を示します。
文字の出現頻度表
| 文字 | z | k | m | c | u | d | l | e |
| 頻度 | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
ハフマン符号の割り当て結果
上記の頻度表をもとにハフマン木を構築すると、頻度の高い文字ほど短い符号が割り当てられます。結果は次の表のようになります。
| 文字 | 頻度 | 符号 | ビット数 |
|---|---|---|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
ハフマン木の図解
上記の例に対応するハフマン木は以下の通りです。頻度の最も高い「e」が根に近い浅い位置に置かれ、頻度の低い「z」「k」は深い位置に配置されていることが分かります。
-
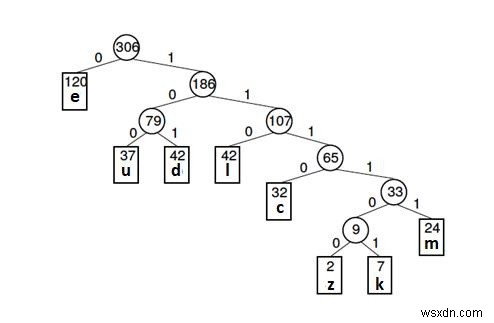
データ構造の範囲ツリー(レンジツリー)とは?仕組み・kd-treeとの違い・構築方法を解説
範囲ツリー(range tree)は、点の集合を格納するための順序付き木構造として定義されるデータ構造です。最大の特徴は、指定された範囲内に存在するすべての点を効率的に取得できる点にあり、実務では主に2次元以上の空間で実装されます。範囲ツリーはkd-tree(kd木)とよく似た構造を持っていますが、両者には明確なトレードオフがあります。範囲ツリーはクエリ時間が O(logd n + k) とkd-treeより高速である一方、必要な記憶領域は O(n logd-1 n) と大きくなります。ここで、d は空間の次元数、n は木に格納されている点の総数、k は1回のクエリで取得される点の数を表します
-
データ構造における高さ制限付きハフマンツリーの基礎と実装上の課題
高さ・深さ制限付きハフマンツリーとは 高さ（深さ）に制限を設けたハフマンツリーの構成図は、下図のとおりです。 木の深さの制限は一見単純な問題に思われますが、実際のハフマン符号化の実装においては、多くの場合に対処すべき重要な課題となります。 標準的なハフマン構築には深さの制限がない 標準的なハフマン木の構築アルゴリズムは、木の高さや深さを一切制限しません。仮に深さを制限すると、「最適（オプティマル）」な符号 rather ではなくなるためです。ただし、ハフマン木の最大深度はフィボナッチ数列によって理論的な上限が定められており、際限なく深くなることはありません。それでも、実用上望まれる深さを大