データ構造の平衡二分探索木
ここでは、平衡二分探索木とは何かを確認します。二分探索木(BST)は二分木であり、左の子では要素が少なく、右の子では要素が大きくなります。
BSTで要素を検索するための平均時間計算量はO(log n)です。二分探索木の高さに依存します。二分探索木の特性を維持するために、木が歪むことがあります。したがって、歪んだ木は次のようになります-
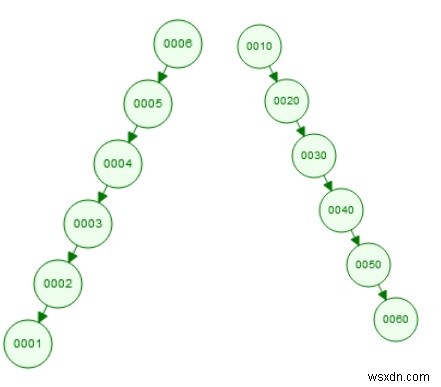
これは実際にはツリーですが、リンクリストのように見えます。この種の木の場合、検索時間はO(n)になります。これは二分木には効果的ではありません。
これらの問題を克服するために、高さのバランスが取れたツリーを作成できます。したがって、木は殺されません。力強く、バランスを取ります。したがって、ノードの両側には、高さがほぼ同じになるサブツリーが保持されます
バランスを取るにはさまざまな手法があります。それらのいくつかは-
です-
AVLツリー
-
赤黒木
上記の例の高さバランスのとれたフォームは次のようになります-
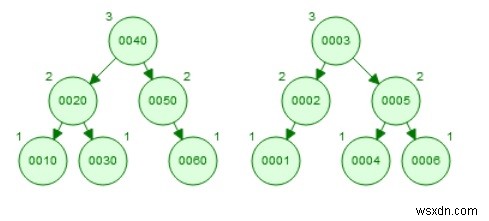
-
データ構造の二分探索木
二分探索木は、いくつかの特性を持つ二分木です。これらのプロパティは次のようなものです- すべての二分探索木は二分木です 左の子はすべて、ルートよりも価値が低くなります すべての正しい子はrootよりも大きな価値を持ちます 理想的な二分探索木は、同じ値を2回保持することはありません。 このようなツリーが1つあるとします- このツリーは1つの二分探索木です。上記のすべてのプロパティに従います。要素をインオーダートラバーサルモードにトラバースすると、5、8、10、15、16、20、23を取得できます。これをC++コードで実装する方法を理解するために1つのコードを見てみましょう。 例 #
-
データ構造の二分木とプロパティ
このセクションでは、1つの二分木データ構造のいくつかの重要なプロパティを確認します。このような二分木があるとします。 一部のプロパティは-です レベル「l」のノードの最大数は$2^{l-1}$になります。ここで、レベルは、ルート自体を含む、ルートからノードへのパス上のノードの数です。ルートのレベルは1であると考えています。 高さhの二分木に存在するノードの最大数は$2^ {h}-1$です。ここで、heightは、ルートからリーフへのパス上のノードの最大数です。ここでは、1つのノードを持つ木の高さが1であると考えています。 n個のノードを持つ二分木では、可能な最小の高さまたは最小のレ
