データ構造のスレッド化された二分木
1つのノードに空いている左または右の子領域がある場合、それはスレッドとして使用されます。スレッド化された二分木には2つのタイプがあります。シングルスレッドツリーまたはフルスレッドバイナリツリー。シングルスレッドモードでは、さらに2つのバリエーションがあります。左ネジと右ネジ。
あるノードに左の子がない場合の左スレッドモードでは、左のポインタはその順序の先行を指します。同様に、あるノードに右の子がない場合の右のスレッドモードでは、右のポインタはその順序の後続を指します。どちらの場合も、後続または先行が存在しない場合は、ヘッダーノードを指します。
完全にスレッド化されたバイナリツリーの場合、各ノードには5つのフィールドがあります。通常の二分木ノードのような3つのフィールド、その側のリンクが実際のリンクであるかスレッドであるかを示すブール値を格納するための別の2つのフィールド。
| 左スレッドフラグ | 左リンク | データ | 右リンク | 右スレッドフラグ |
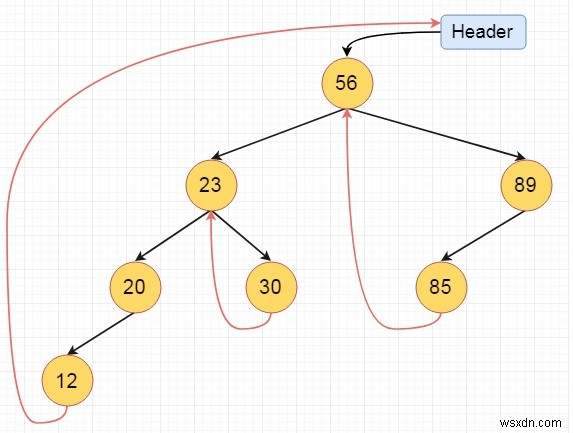
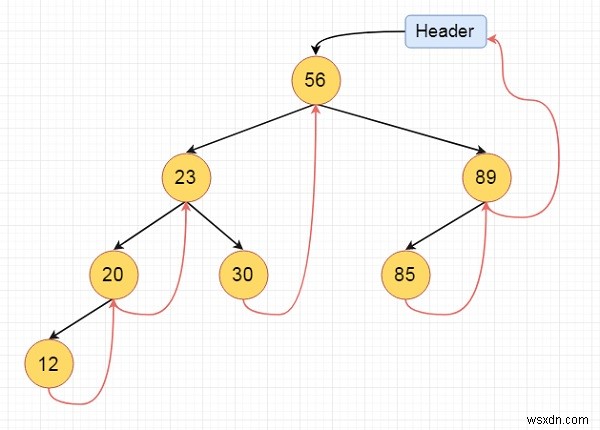
これは完全にスレッド化された二分木です
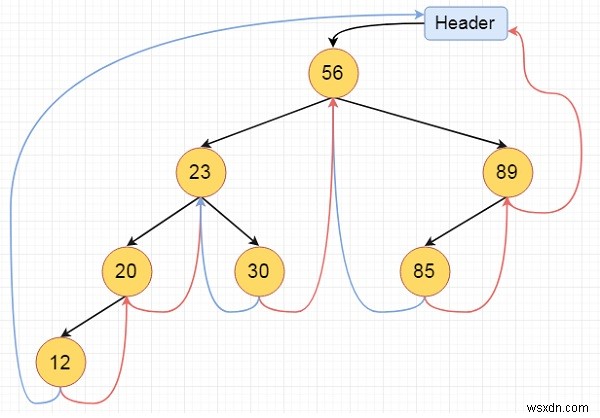
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
-
データ構造の二分木とプロパティ
このセクションでは、1つの二分木データ構造のいくつかの重要なプロパティを確認します。このような二分木があるとします。 一部のプロパティは-です レベル「l」のノードの最大数は$2^{l-1}$になります。ここで、レベルは、ルート自体を含む、ルートからノードへのパス上のノードの数です。ルートのレベルは1であると考えています。 高さhの二分木に存在するノードの最大数は$2^ {h}-1$です。ここで、heightは、ルートからリーフへのパス上のノードの最大数です。ここでは、1つのノードを持つ木の高さが1であると考えています。 n個のノードを持つ二分木では、可能な最小の高さまたは最小のレ
