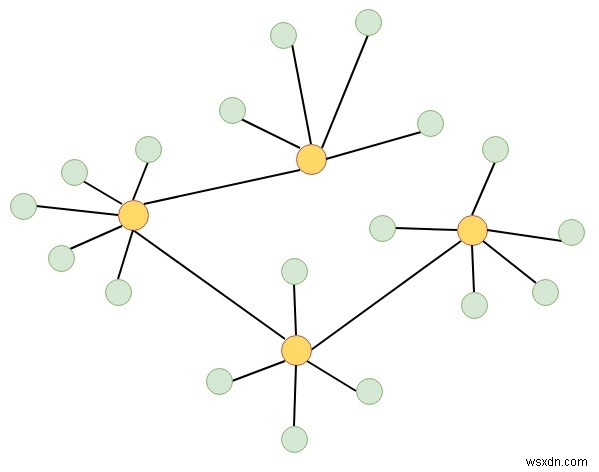
データ構造の根なし二分木
ここでは、根なし二分木とは何かを確認します。これらのツリーは、サイクルのない無向グラフに接続されています。隣接する頂点が1つある頂点は、木の葉です。残りの頂点は内部ノードです。頂点の次数は、隣接する頂点の数です。複数のノードを持つツリーでは、葉は1次の頂点です。
フリーツリーはバイナリツリーの一種であり、すべての内部ノードの次数は正確に3です。コンピュータサイエンスでは、データ構造として使用される場合、バイナリツリーはルート化され、順序付けられることがよくありますが、階層的クラスタリングおよび進化的ツリー再構築におけるルート化されていないバイナリツリーのアプリケーションは重要です。
-
データ構造の仮想ツリーでのスプレー
仮想ツリーでは、一部のエッジは実線として扱われ、一部は破線として扱われます。通常のスプレイは、堅い木でのみ実行されます。仮想ツリーのノードyで表示するには、次の方法を実装します。 アルゴリズムは、パスごとに1回ずつ、ツリーを3回調べ、それを変更します。最初のパスでは、ノードyから開始して、ソリッドツリーのみでスプレイすることにより、yからツリー全体のルートへのパスが破線になります。このパスは、スプライシングによって確実に作成されます。ノードyでの最後のスプレイにより、yがツリーのルートになります。非公式ではありませんが、アルゴリズムは次のように説明されています Splay(y)のアルゴリズ
-
データ構造における二分木表現
ここでは、コンピュータのメモリでバイナリツリーを表現する方法を説明します。表現するには2つの異なる方法があります。これらは配列とリンクリストを使用しています。 このようなツリーが1つあるとします- 配列表現は、レベル順の方法を使用して要素をスキャンすることにより、ツリーデータを格納します。したがって、ノードをレベルごとに格納します。一部の要素が欠落している場合は、空白のままにします。上記のツリーの表現は以下のようになります- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 10 5