データ構造の二項ヒープ
二項ヒープは、二項ツリーのコレクションです。二項ツリーBkは、再帰的に定義された順序付きツリーです。二項ツリーB0は、単一のノードで構成されています。
二項ツリーBkは、2つの二項ツリーBk-1で構成されます。それは一緒にリンクされています。一方のルートは、もう一方のルートの左端の子です
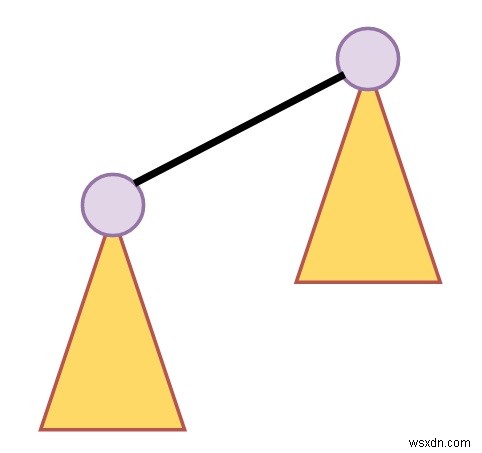
いくつかの二項ヒープは以下のようなものです-
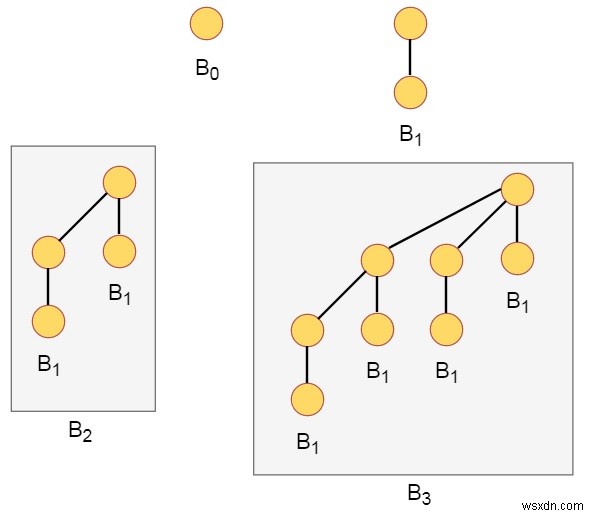
二項ツリーのいくつかのプロパティは次のとおりです-
-
B kの二項ツリー 2 kがあります ノード。
-
木の高さはkです
-
0からkの範囲のすべてのiについて、深さiに正確に$$ \ left(\ begin {array} {c} k \\ j \ end {array} \ right)$$ノードがあります
二項ヒープHは、二項ツリーのセットです。いくつかのプロパティがあります。
-
Hの各二項ツリーはヒープ順になっています。したがって、ノードのキーはその親のキー以上です。
-
Hには最大で1つの二項木があり、その根には一定の次数があります。
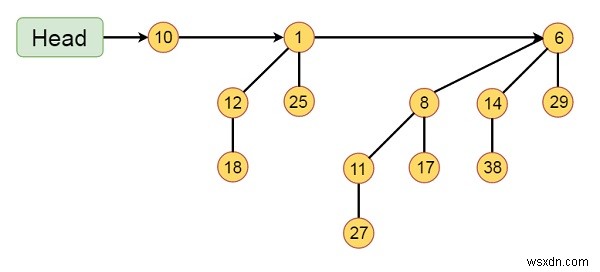
この二項ヒープHは、二項ツリーB0、B2、およびB3で構成されます。それぞれ1、4、8ノードです。そして合計でn=13ノード。二項ツリーのルートは、リンクリストによって次数の昇順でリンクされています
-
データ構造のBSPツリー
コンピュータサイエンスでは、超平面をパーティションとして実装することにより、空間を2つの凸集合に再帰的に分割するために、バイナリ空間分割(BSP)と呼ばれる方法が実装されています。この細分化のプロセスにより、BSPツリーと呼ばれるツリーデータ構造の形式で領域内のオブジェクトが表現されます。 バイナリ空間分割は、1969年に3Dコンピュータグラフィックスのコンテキストで発明されました。BSPツリーの構造により、レンダリングに役立つシーン内のオブジェクトに関する空間情報が可能になります。たとえば、オブジェクトは前から後ろに並べられます。すばやくアクセスできるように、特定の場所にいる視聴者を尊重し
-
データ構造の仮想ツリーでのスプレー
仮想ツリーでは、一部のエッジは実線として扱われ、一部は破線として扱われます。通常のスプレイは、堅い木でのみ実行されます。仮想ツリーのノードyで表示するには、次の方法を実装します。 アルゴリズムは、パスごとに1回ずつ、ツリーを3回調べ、それを変更します。最初のパスでは、ノードyから開始して、ソリッドツリーのみでスプレイすることにより、yからツリー全体のルートへのパスが破線になります。このパスは、スプライシングによって確実に作成されます。ノードyでの最後のスプレイにより、yがツリーのルートになります。非公式ではありませんが、アルゴリズムは次のように説明されています Splay(y)のアルゴリズ
