データ構造の赤黒木への挿入

赤黒木は、ツリーの各ノードが赤または黒で色付けされた平衡二分探索木です。赤黒木で実行できる操作には、検索、挿入、削除の3種類があります。

次の赤黒木に要素を挿入する必要があるとしましょう。

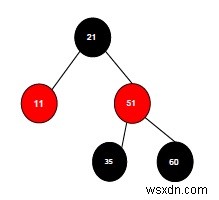
赤黒木に要素を挿入する方法は非常に簡単です。通常の二分木に挿入するのと同じように挿入を実行します。ルートノードから開始して、ノードの色を確認し、特定の位置に挿入します。ただし、赤黒木では、要素を挿入するための追加の手順が必要です。

ただし、条件に従うと、赤黒木はバランスが取れていることを知っておく必要があります-

• すべてのルートノードは黒である必要があります。

• すべてのノードは赤または黒です。

• ノードが赤の場合、その子は黒である必要があります。

• ルートからエンドまでのパスには、同数のブラックノードが含まれている必要があります。

赤黒木に新しいノードを挿入する場合は、挿入手順を確認することで挿入できます。

赤黒木に要素を挿入する手順-

• ツリーが空かどうかを確認します。ツリーが空の場合は、新しいノードを挿入し、それを黒に色付けします。 （ルートノードの色は常に黒である必要があるため）」

• それ以外の場合、ツリーが空でない場合は、新しいノードをリーフノードとして最後まで挿入し、赤で色付けします。

• 新しいノードの親が赤で、その隣接（親）ノードも赤の場合、隣接ノードと親および祖父母の両方の色を反転します（ルートノードでない場合は、親と隣接ノードの色のみを反転します）。 、黒。

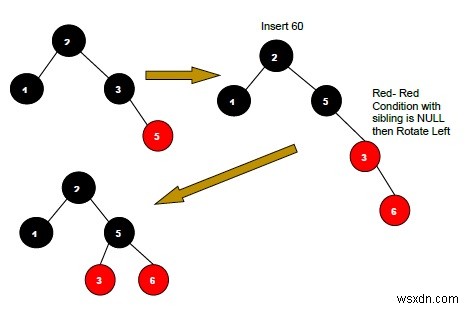
• 新しいノードの親が赤で、その隣接する（親の）ノードが空またはNULLの場合、新しいノードと親を回転（左左または左右回転）します。

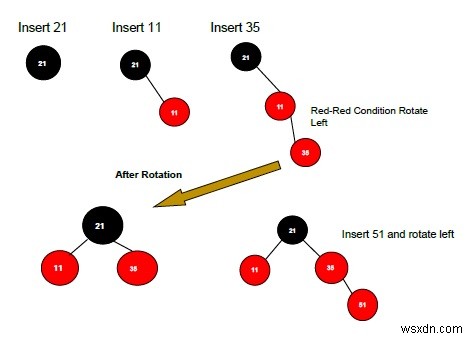
適用される回転には、左左回転と左右回転の2種類があります。ローテーションは、一部の条件でのみ適用されます。条件は-

• 新しいノードの親が赤で、隣接ノードが空またはNULLの場合は、左または右に回転します。

• 左左回転で、親と祖父母の色を反転します。親を祖父母、祖父母を子にします。

アルゴリズム

RBTreeInsertion（root、key）

//The color of the inserted new node is Red
color[key] <- Red
while(key≠root and color (p[key]=Red))
do if p[key]= left(p[p[key]])
   Then y←right[p[p[key]]
// If the parent of the new node is Red(if there is Grandparent instead
root Node) Flip the color.
   if color[y]← Red
   then color(p[key])← Black
      color(p[p[key]])← Red
      key← p[p[key]]
   else if key← right[p[key]]
      then key← p[key]
      //When parent of new node has the red color and its sibling is NULL
   LeftRotate(root,key)
   color(p[key]) ← Black
   color(p[p[key]]) ← Red
RotateRight(root,p[p[key]])
else exchange then left and right elements to make it balance.
color(root)← Black