データ構造で式ツリーを構築するためのアルゴリズム
式ツリー
式ツリーは、リーフノードが操作される値を持ち、内部ノードがリーフノードが実行される演算子を含むツリーです。
例
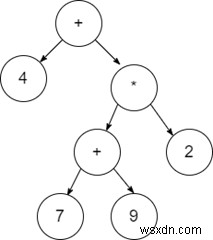
4 +((7 + 9)* 2) 次のような式ツリーがあります
式ツリーを構築するためのアルゴリズム
Tを式ツリーとします。
If T is not NULL:
If T->data is an operand:
return T.data
A = solve(T.left)
B = solve(T.right)
--> Calculate operator for 'T.data' on A and B, and call recursively,
return calculate(A, B, T.data)
式ツリーを作成するにはどうすればよいですか?
特定の式の式ツリーを構築するには、通常、スタックデータ構造を使用します。
最初に、指定された接尾辞式を繰り返し処理し、以下の手順に従います-
- 指定された式でオペランドを取得した場合は、それをスタックにプッシュします。これは、式ツリーのルートになります。
- 演算子が式で2つの値を取得した場合は、式ツリーにその子として追加し、それらを現在のノードにプッシュします。
- 指定された式が完了しなくなるまで、ステップ1とステップ2を繰り返します。
- ここで、すべてのルートノードにオペランドしか含まれておらず、すべての子ノードに値のみが含まれているかどうかを確認します。
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
-
データ構造の仮想ツリーでのスプレー
仮想ツリーでは、一部のエッジは実線として扱われ、一部は破線として扱われます。通常のスプレイは、堅い木でのみ実行されます。仮想ツリーのノードyで表示するには、次の方法を実装します。 アルゴリズムは、パスごとに1回ずつ、ツリーを3回調べ、それを変更します。最初のパスでは、ノードyから開始して、ソリッドツリーのみでスプレイすることにより、yからツリー全体のルートへのパスが破線になります。このパスは、スプライシングによって確実に作成されます。ノードyでの最後のスプレイにより、yがツリーのルートになります。非公式ではありませんが、アルゴリズムは次のように説明されています Splay(y)のアルゴリズ
