データ構造における高さバイアスの左翼ツリー
ここでは、Height Balanced Leftist Trees(HBLT)とは何かを確認します。 外部ノードと呼ばれる特別なノードがある二分木を考えてみましょう。 空の各サブツリーを置き換えます。他のすべてのノードは内部ノードと呼ばれます 。いくつかの外部ノードがいくつかのバイナリツリーとともに追加される場合、それは拡張バイナリツリーと呼ばれます。 。
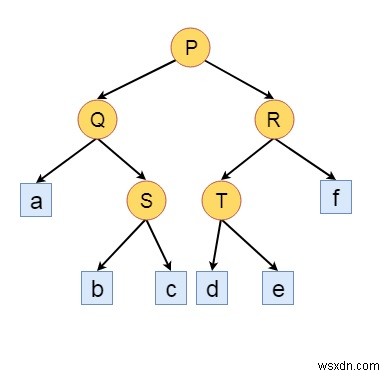
このツリーの葉の端を考慮しない場合、それは実際の二分木です。これは拡張された二分木です。
ここで、 s(x) ノードxからそのサブツリー内の外部ノードまでの最短経路の長さです。 xが外部ノードの場合、その s(x) 値は0です。xが内部ノードの場合、値は-
です。min{𝑠(𝐿), 𝑠(𝑅)} + 1 ここで、LとRはxの左右の子です。次に、指定されたツリーのs値を確認しましょう。
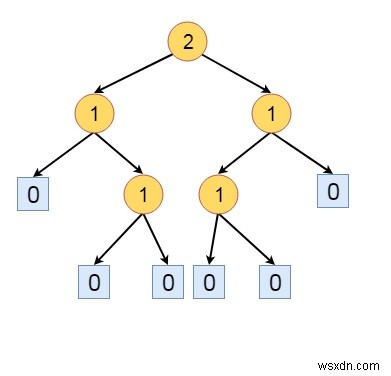
HBLTの定義は次のようになります。バイナリツリーは、すべての内部ノードで、左の子のs値が右の子のs値以上である場合に限り、高さバランスのとれた左利きツリー(HBLT)です。
上記のツリーはHBLTではありません。ノードaの親は、s(L)=0であり、s(R)は1です。ただし、他のすべてのノードはHBLTのルールを満たしています。したがって、そのノードのサブツリーを左右に移動すると、HBLTになります。
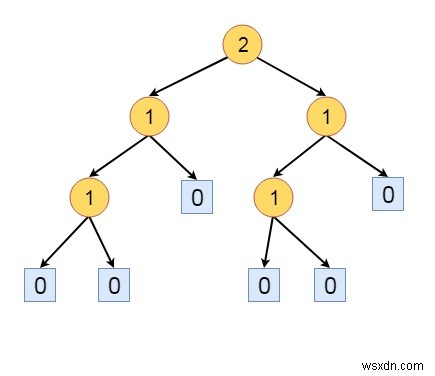
他のいくつかの定義は-
です-
最大ツリー(最小ツリー)は、各ノードの値がその子よりも大きい(小さい)か等しいツリーです。
-
最大HBLTはHBLTであり、これは最大ツリーでもあり、最小HBLTはHBLTであり、最小ツリーでもあります。
-
データ構造のBSPツリー
コンピュータサイエンスでは、超平面をパーティションとして実装することにより、空間を2つの凸集合に再帰的に分割するために、バイナリ空間分割(BSP)と呼ばれる方法が実装されています。この細分化のプロセスにより、BSPツリーと呼ばれるツリーデータ構造の形式で領域内のオブジェクトが表現されます。 バイナリ空間分割は、1969年に3Dコンピュータグラフィックスのコンテキストで発明されました。BSPツリーの構造により、レンダリングに役立つシーン内のオブジェクトに関する空間情報が可能になります。たとえば、オブジェクトは前から後ろに並べられます。すばやくアクセスできるように、特定の場所にいる視聴者を尊重し
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
