データ構造における重みバイアス左翼ツリー
これは、重みバイアス左翼ツリー(WBLT)の例です-
二分木が次のようになっていると仮定します-
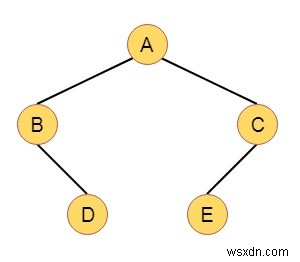
各ノードのw(x)値を計算すると、次のようになります-
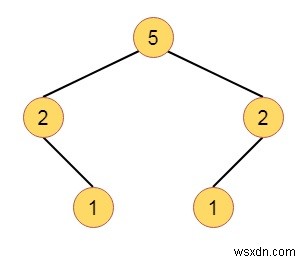
これで、WBLTの定義は次のようになります-
二分木は、すべての内部ノードで、左の子のw(x)が右の子のw(x)以上である場合にのみ、Weight BalancedLeftistTreeと呼ばれます。最大(最小)WBLTは、WBLTでもある最大(最小)ツリーです。
-
データ構造のBSPツリー
コンピュータサイエンスでは、超平面をパーティションとして実装することにより、空間を2つの凸集合に再帰的に分割するために、バイナリ空間分割(BSP)と呼ばれる方法が実装されています。この細分化のプロセスにより、BSPツリーと呼ばれるツリーデータ構造の形式で領域内のオブジェクトが表現されます。 バイナリ空間分割は、1969年に3Dコンピュータグラフィックスのコンテキストで発明されました。BSPツリーの構造により、レンダリングに役立つシーン内のオブジェクトに関する空間情報が可能になります。たとえば、オブジェクトは前から後ろに並べられます。すばやくアクセスできるように、特定の場所にいる視聴者を尊重し
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
