プリム（最小スパニングツリー）MSTアルゴリズム

連結グラフG（V、E）があり、すべてのエッジの重みまたはコストが示されています。プリムのアルゴリズムは、グラフGから最小全域木を見つけます。

成長するツリーアプローチです。このアルゴリズムでは、ツリーを開始するためにシード値が必要です。シード頂点は、ツリー全体を形成するように成長します。

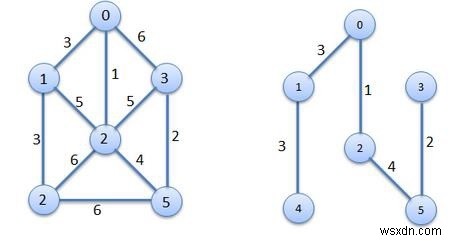
この問題は、2つのセットを使用して解決されます。 1つのセットには、すでに選択されているノードが保持され、別のセットには、まだ考慮されていないアイテムが保持されます。シード頂点から、最小エッジコストに基づいて隣接する頂点を取得するため、ノードを1つずつ取得してツリーを成長させます。

• この問題の時間計算量はO（V2）です。ここで、Vは頂点の数です。

入力 −隣接リスト−

出力-

(0)---(1|1) (0)---(2|3) (0)---(3|4)
(1)---(0|1) (1)---(4|2)
(2)---(0|3)
(3)---(0|4)
(4)---(1|2) (4)---(5|2)
(5)---(4|2) (5)---(6|3)
(6)---(5|3)

アルゴリズム

prims（g：グラフ、t：ツリー、開始）

入力 −グラフg、空白のツリーと「開始」という名前のシード頂点出力：エッジを追加した後のツリー。

Begin
   define two sets as usedVert, unusedVert
   usedVert[0] := start and unusedVert[0] := φ
   for all vertices except start do
      usedVert[i] := φ
      unusedVert[i] := i //add all vertices in unused list
   done
   while number of vertices in usedVert ≠ V do //V is number of total nodes
      min := ∞
      for all vertices of usedVert array do
         for all vertices of the graph do
            if min > cost[i,j] AND i ≠ j then
               min := cost[i,j]
               ed := edge between i and j, and cost of ed := min
            done
         done
         unusedVert[destination of ed] := φ
         add edge ed into the tree t
         add source of ed into usedVert
   done
End

例（C ++）

#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
   {0, 1, 3, 4, INF, 5, INF},
   {1, 0, INF, 7, 2, INF, INF},
   {3, INF, 0, INF, 8, INF, INF},
   {4, 7, INF, 0, INF, INF, INF},
   {INF, 2, 8, INF, 0, 2, 4},
   {5, INF, INF, INF, 2, 0, 3},
   {INF, INF, INF, INF, 4, 3, 0}
};
typedef struct{
   int u, v, cost;
}edge;
class Tree{
   int n;
   edge edges[V-1]; //as a tree has vertex-1 edges
   public:
   Tree(){
      n = 0;
   }
   void addEdge(edge e){
      edges[n] = e; //add edge e into the tree
      n++;
   }
   void printEdges(){ //print edge, cost and total cost
      int tCost = 0;
      for(int i = 0; i<n; i++){
         cout << "Edge: " << char(edges[i].u+'A') < "--" << char(edges[i].v+'A');
         cout << " And Cost: " << edges[i].cost << endl;
         tCost += edges[i].cost;
      }
      cout << "Total Cost: " << tCost << endl;
   }
   friend void prims(Tree &tre, int start);
};
void prims(Tree &tr, int start){
   int usedVert[V], unusedVert[V];
   int i, j, min, p;
   edge ed;
   //initialize
   usedVert[0] = start; p = 1;
   unusedVert[0] = -1;//-1 indicates the place is empty
   for(i = 1; i<V; i++){
      usedVert[i] = -1;//all places except first is empty
      unusedVert[i] = i;//fill with vertices
   }
   tr.n = 0;
   //get edges and add to tree
   while(p != V){ //p is number of vertices in usedVert array
      min = INF;
      for(i = 0; i<p; i++){
         for(j = 0; j<V; j++){
            if(unusedVert[j] != -1){
               if(min > costMat[i][j] && costMat[i][j] != 0){
                  //find the edge with minimum cost
                  //such that u is considered and v is not considered yet
                  min = costMat[i][j];
                  ed.u = i; ed.v = j; ed.cost = min;
               }
            }
         }
      }
      unusedVert[ed.v] = -1;//delete v from unusedVertex
      tr.addEdge(ed);
      usedVert[p] = ed.u; p++;//add u to usedVertex
   }
}
main(){
   Tree tr;
   prims(tr, 0); //starting node 0
   tr.printEdges();
}

出力

(0)---(1|1) (0)---(2|3) (0)---(3|4)
(1)---(0|1) (1)---(4|2)
(2)---(0|3)
(3)---(0|4)
(4)---(1|2) (4)---(5|2)
(5)---(4|2) (5)---(6|3)
(6)---(5|3)