Excelで複利を計算する方法

皆さんは、学校の複利を計算する式を学びました。 複雑で単純な利益 実生活で何年も使用されてきた数学的アプリケーションの1つです。私たちの生活の特定の例では、単純な複利を計算する必要があります。たとえば、金融会社や友人から一定の利率でお金を借りる場合、だまされないように、複合利子と単利の計算を知っておく必要があります。

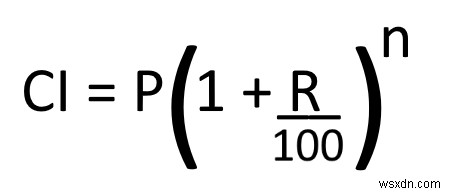
Excel で複利を計算する方法を知っている場合は、紙の複利を計算する以外に 、それはあなたのプロ意識に追加の利点になります。上記の式で、Pは主値、Rは利率、nは合計時間です。

ここでは、Excelを使用して複利を計算する方法を学習します。ただし、始める前に、複利計算で使用される用語を見てみましょう。

• 毎年または毎年複合 ：ここでは、利率が毎年元本に適用されます。
• 半年ごとまたは半年ごとに作成 ：ここでは、6か月ごとに元本値が増加します。つまり、年に2回です。半年ごとに複利を計算するには、nに2を掛け、利率を2で割る必要があります。
• 四半期ごとに作成 ：毎年4つの四半期があります。ここでは、元本値は3か月ごと、つまり1年に4回ごとに増加します。四半期ごとに複利を計算するには、nに4を掛け、利率を4で割る必要があります。
• 毎月複合 ：1年に12ヶ月あります。したがって、毎月複合とは、利息が毎月適用されることを意味します。したがって、nに12を掛け、利率を12で割る必要があります。

Excelで複利（CI）を計算する方法

ここで説明します：

1. 利率が毎年複利になる場合。
2. 利率が半年ごとに合成される場合。
3. 利率が四半期ごとに合成される場合。
4. 利率が毎月複合される場合。

Excelで複利の計算を見てみましょう。

1]Excelで毎年複利計算する

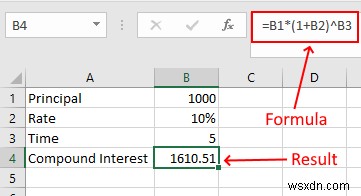
次の値のサンプルデータを見てみましょう。

• P =1000
• R =10％
• n=5年

上記のデータをExcelに入力し、次の数式を記述します。

=B1*(1+B2)^B3

B1、B2、およびB3は、それぞれ主値、利率、および時間を示すセルアドレスです。セルアドレスを正しく入力してください。正しく入力しないと、エラーが発生します。

2]Excelで半年ごとに複利計算する

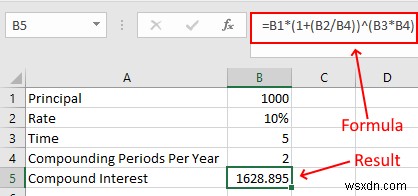
ここでは、データにもう1つの値を追加して、1年あたりの複利計算を行う必要があります。上で説明したように、2年半は1年になります。したがって、半年ごとに2つの複利計算期間があります。

• プリンシパル=1000
• 利率=10％
• 時間=5年
• 1年あたりの複利計算期間=2

上記のデータをExcelに入力し、次の数式を記述します。

=B1*(1+(B2/B4))^(B3*B4)

ほら、利率（B2セルの値）を2（B4セルの値）で割り、時間（B3セルの値）に2（B4セルの値）を掛けました。

3]Excelで四半期ごとに複利計算する

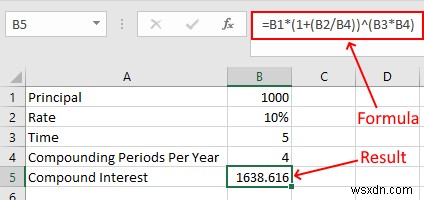
ここでは、半年ごとのCIの計算に使用した式は同じままです。ここで、それぞれのセルの値を変更する必要があります。四半期ごとのCI計算では、B4セルの値を4に変更します。

4]Excelで毎月複利計算する

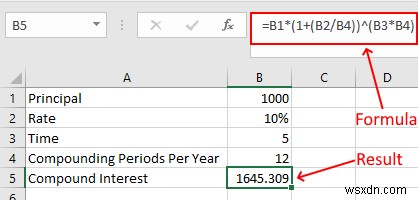
毎月複合される利息を計算するには、B4セルの値を12に変更し、同じ数式を使用します。

それでおしまい。 ExcelでのCIの計算について質問がある場合は、お知らせください。

次を読む ：Excelで単利を計算する方法。