C++でのスレッド化された二分木の順序のないトラバーサル

ここでは、スレッド化された二分木データ構造を確認します。二分木ノードには最大で2つの子が存在する可能性があることがわかっています。ただし、子が1つしかない場合、または子がない場合、リンクリスト表現のリンク部分はnullのままになります。スレッド化された二分木表現を使用して、いくつかのスレッドを作成することにより、その空のリンクを再利用できます。

1つのノードに空いている左または右の子領域がある場合、それはスレッドとして使用されます。スレッド化された二分木には2つのタイプがあります。シングルスレッドツリーまたはフルスレッドバイナリツリー。

完全にスレッド化されたバイナリツリーの場合、各ノードには5つのフィールドがあります。通常の二分木ノードのような3つのフィールド、その側のリンクが実際のリンクであるかスレッドであるかを示すブール値を格納するための別の2つのフィールド。

これは完全にスレッド化された二分木です

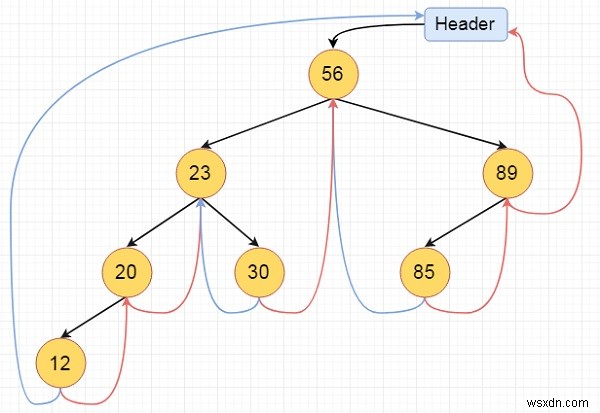
アルゴリズム

inorder():
Begin
   temp := root
   repeat infinitely, do
   p := temp
   temp = right of temp
   if right flag of p is false, then
      while left flag of temp is not null, do
         temp := left of temp
      done
   end if
   if temp and root are same, then
      break
   end if
      print key of temp
   done
End

例

#include <iostream>
#define MAX_VALUE 65536
using namespace std;
class N { //node declaration
   public:
      int k;
      N *l, *r;
      bool leftTh, rightTh;
};
class ThreadedBinaryTree {
   private:
   N *root;
   public:
   ThreadedBinaryTree() { //constructor to initialize the variables
      root= new N();
      root->r= root->l= root;
      root->leftTh = true;
      root->k = MAX_VALUE;
   }
   void insert(int key) {
      N *p = root;
      for (;;) {
      if (p->k< key) { //move to right thread
         if (p->rightTh)
            break;
         p = p->r;
      }
      else if (p->k > key) { // move to left thread
         if (p->leftTh)
            break;
         p = p->l;
      }
      else {
         return;
      }
   }
   N *temp = new N();
   temp->k = key;
   temp->rightTh= temp->leftTh= true;
   if (p->k < key) {
      temp->r = p->r;
      temp->l= p;
      p->r = temp;
      p->rightTh= false;
   }
   else {
      temp->r = p;
      temp->l = p->l;
      p->l = temp;
      p->leftTh = false;
   }
}
void inorder() { //print the tree
   N *temp = root, *p;
   for (;;) {
      p = temp;
      temp = temp->r;
      if (!p->rightTh) {
         while (!temp->leftTh) {
            temp = temp->l;
         }
      }
      if (temp == root)
         break;
         cout<<temp->k<<" ";
      }
      cout<<endl;
   }
};
int main() {
   ThreadedBinaryTree tbt;
   cout<<"Threaded Binary Tree\n";
   tbt.insert(56);
   tbt.insert(23);
   tbt.insert(89);
   tbt.insert(85);
   tbt.insert(20);
   tbt.insert(30);
   tbt.insert(12);
   tbt.inorder();
   cout<<"\n";
}

出力

Threaded Binary Tree
12 20 23 30 56 85 89