C++での二分木最長連続シーケンスII

二分木があるとしましょう。その二分木で最長の連続パスの長さを見つける必要があります。ここで、パスは増加または減少する可能性があります。したがって、例として、[1,2,3,4]と[4,3,2,1]は両方とも有効なパスと見なされますが、パス[1,2,4,3]は有効なパスではありません。

それ以外の場合、パスは子-親-子の順序になる可能性がありますが、必ずしも親子の順序である必要はありません。

したがって、入力が次のような場合

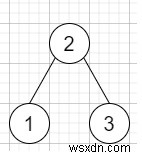
最長の連続パスは[1、2、3]または[3、2、1]のようになるため、出力は3になります。

これを解決するには、次の手順に従います-

• 関数solveUtil（）を定義します。これはノードを取ります

• ノードがnullの場合、-

  • 戻り値{0、0}

• 左=solveUtil（ノードの左側）

• 左=solveUtil（ノードの右）

• 1つのペアの温度を定義します：={1,1}

• ノードの左側が存在し、ノードの左側の値がノードの値+ 1と同じである場合、-

  • temp.first：=temp.firstと1+ left.first

    の最大値

  • ans：=ansとtemp.firstの最大値

• ノードの権利が存在し、ノードの権利の値がノードの値+ 1と同じである場合、-

  • temp.first：=temp.firstと1+ right.first

    の最大値

  • ans：=ansとtemp.firstの最大値

• ノードの左側が存在し、ノードの左側の値がノード-1の値と同じである場合、-

  • temp.second：=temp.secondの最大値と1+ left.second

  • ans：=ansとtemp.secondの最大値

• ノードの権利が存在し、ノードの権利の値がノードの値-1と同じである場合、-

  • temp.second：=temp.secondの最大値と1+ right.second

  • ans：=ansとtemp.secondの最大値

• ans：=最大{ans and temp.first + temp.second-1}

• 温度を返す

• メインの方法から、次のようにします-

• ans：=0

• resolveUtil（root）

• ansを返す

例

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = NULL;
      right = NULL;
   }
};
class Solution {
public:
   int ans = 0;
   pair<int, int> solveUtil(TreeNode* node){
      if (!node) {
         return { 0, 0 };
      }
      pair<int, int> left = solveUtil(node->left);
      pair<int, int> right = solveUtil(node->right);
      pair<int, int> temp = { 1, 1 };
      if (node->left && node->left->val == node->val + 1) {
         temp.first = max(temp.first, 1 + left.first);
         ans = max(ans, temp.first);
      }
      if (node->right && node->right->val == node->val + 1) {
         temp.first = max(temp.first, 1 + right.first);
         ans = max(ans, temp.first);
      }
      if (node->left && node->left->val == node->val - 1) {
         temp.second = max(temp.second, 1 + left.second);
         ans = max(ans, temp.second);
      }
      if (node->right && node->right->val == node->val - 1) {
         temp.second = max(temp.second, 1 + right.second);
         ans = max(ans, temp.second);
      }
      ans = max({ ans, temp.first + temp.second - 1 });
      return temp;
   }
   int longestConsecutive(TreeNode* root){
      ans = 0;
      solveUtil(root);
      return ans;
   }
};
main(){
   Solution ob;
   TreeNode *root = new TreeNode(2);
   root->left = new TreeNode(1);
   root->right = new TreeNode(3);
   cout << (ob.longestConsecutive(root));
}

入力

TreeNode *root = new TreeNode(2);
root->left = new TreeNode(1);
root->right = new TreeNode(3);

出力

3