C++で配列のビットノイズをチェックするプログラム

N個の整数の配列arr[N]が与えられた場合、タスクは、与えられた配列がバイトニックであるかどうかをチェックすることです。指定されたアレイがバイトニックである場合は、「はい、バイトニックアレイです」と出力します。そうでない場合は、「いいえ、バイトニックアレイではありません」と出力します。

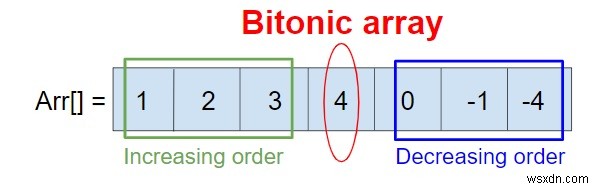
Bitonicアレイとは、アレイが最初に厳密に昇順で、次に厳密に降順である場合です。

この配列のように、arr [] ={1、2、3、4、2、-1、-5}はバイトニック配列です。これは、4までは厳密に昇順であり、4以降は厳密に降順であるためです。

入力

arr[] = {1, 3, 5, 4, 2, 0}

出力

Yes its a bitonic array

説明

1< 3 < 5 > 4 > 2 >0, so yes it is a bitonic array.

入力

arr[] = {1, 2, 3, 4, 5, 0, -1, -2, 6, -4}

出力

No its not a bitonic array

問題を解決するために以下で使用するアプローチは次のとおりです

• 配列のすべての要素を繰り返し、前の要素が現在の要素よりも小さいことを確認します。

• 前の要素が現在の要素のブレークより小さくない場合。

• 前の要素が現在の要素よりも大きいかどうかを確認します。そうでない場合は、falseを返し、終了します。

• 配列の最後に達した場合はtrueを返します。

アルゴリズム

Start
Step 1→ Declare array to check for bitonicity of an array
   int check(int arr[], int size)
      declare int i, j
      Loop For i = 1 and i <size and i++
         IF (arr[i] > arr[i - 1])
            Continue
         End
         IF (arr[i] <= arr[i - 1])
            break
         End
         IF(i == size - 1)
            return 1
         End
         Loop For (j = i + 1 and j < size and j++
            IF (arr[j] < arr[j - 1])
               Continue
            End
            IF (arr[j] <= arr[j - 1])
               break
            End
         End
         Set i = j
         IF (i != size)
            return 0
         End
         return 1
Step 2→ In main()
   Declare int arr[] = { -3, 9, 11, 20, 17, 5, 1 }
   Declare int size = sizeof(arr) / sizeof(arr[0])
   Do (check(arr, size) == 1) ? cout << "Yes its a bitonic array" : cout << "no its not a bitonic array"
Stop

例

#include <bits/stdc++.h>
using namespace std;
//function to check bitonic or not
int check(int arr[], int size){
   int i, j;
   for (i = 1; i < size; i++){
      if (arr[i] > arr[i - 1])
         continue;
      if (arr[i] <= arr[i - 1])
         break;
   }
   if (i == size - 1)
      return 1;
   for (j = i + 1; j < size; j++){
      if (arr[j] < arr[j - 1])
         continue;
      if (arr[j] >= arr[j - 1])
         break;
   }
   i = j;
   if (i != size)
      return 0;
   return 1;
}
int main(){
   int arr[] = { -3, 9, 11, 20, 17, 5, 1 };
   int size = sizeof(arr) / sizeof(arr[0]);
   (check(arr, size) == 1) ? cout << "Yes its a bitonic array" : cout << "no its not a bitonic array";
   return 0;
}

出力

上記のコードを実行すると、次の出力が生成されます-

Yes its a bitonic array