C++で二分木の左側面図を見つけるプログラム

二分木があると仮定します。左側からツリーを見ると、そのいくつかの要素を見ることができます。それらの要素を表示する必要があります。したがって、ツリーが次のような場合-

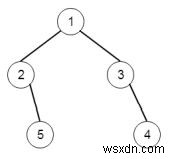
出力は[1,2,5]

これを解決するには、次の手順に従います-

• 配列retを定義する

• 関数dfs（）を定義します。これはノードを取得し、cは1で初期化します

• ノードがnullの場合、-

  • 戻る

• c> lvlの場合、-

  • lvl：=c

  • ノードの値をretに挿入します

• dfs（ノードの左側、c + 1）

• dfs（ノードの右側、c + 1）

• メインの方法から、次のようにします-

• lvl：=-1

• dfs（root、0）

• retを返す

  
  

理解を深めるために、次の実装を見てみましょう-

例

#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<int> v){
   cout << "[";
   for(int i = 0; i<v.size(); i++){
      cout << v[i] << ", ";
   }
   cout << "]"<<endl;
}
class TreeNode{
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = right = NULL;
   }
};
class Solution {
   public:
   vector <int> ret;
   int lvl;
   void dfs(TreeNode* node, int c = 1){
      if(!node)
         return;
      if(c > lvl){
         lvl = c;
         ret.push_back(node->val);
      }
      dfs(node->left, c + 1);
      dfs(node->right, c + 1);
   }
   vector<int> solve(TreeNode* root) {
      lvl = -1;
      dfs(root, 0);
      return ret;
   }
};
main(){
   TreeNode *root = new TreeNode(1);
   root->left = new TreeNode(2);
   root->right = new TreeNode(3);
   root->left->right = new TreeNode(5);
   root->right->right = new TreeNode(4);
   Solution ob;
   print_vector(ob.solve(root));
}

入力

TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->right = new TreeNode(5);
root->right->right = new TreeNode(4);

出力

[1,2,5]