Pythonでバイナリツリーノードの兄弟値を見つけるプログラム

値kと二分探索木があると仮定します。ここでは、各ノードはリーフであるか、2つの子を含みます。値kを含むノードを見つけて、その兄弟の値を返す必要があります。

したがって、入力が次のような場合

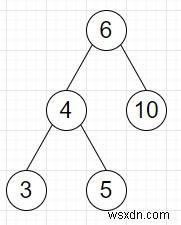
k =4.の場合、出力は10になります。

これを解決するには、次の手順に従います-

• 関数util（）を定義します。これはルート、k、ansを取ります

• ルートの左側がnullでなく、ルートの右側がnullでない場合、

  • 戻る

• k>ルートの値の場合、

  • ルートの権利の値がkと同じである場合、

    • ansの最後にルートの左側の値を挿入します

    • 戻る

  • それ以外の場合

    • util（ルートの権利、k、ans）

• k <ルートの値の場合、

  • ルートの権利の値がkと同じである場合、

    • ansの最後にルートの権利の値を挿入します

    • 戻る

  • それ以外の場合

    • util（ルートの左側、k、ans）

• メインの方法から、次のようにします-

• ans：=新しいリスト

• util（root、k、ans）

• ans [0]

  を返します

理解を深めるために、次の実装を見てみましょう-

例

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.val = data
      self.left = left
      self.right = right

def util(root, k, ans):
   if root.left is None and root.right is None:
      return
   if k > root.val:
      if root.right.val == k:
         ans.append(root.left.val)
         return
      else:
         util(root.right, k, ans)
   if k < root.val:
      if root.left.val == k:
         ans.append(root.right.val)
         return
      else:
         util(root.left, k, ans)

class Solution:
   def solve(self, root, k):
      ans = []
      util(root, k, ans)
      return ans[0]

root = TreeNode(6)
root.left = TreeNode(4)
root.right = TreeNode(10)
root.left.left = TreeNode(3)
root.left.right = TreeNode(5)
ob1 = Solution()
print(ob1.solve(root, 4))

入力

root = TreeNode(6)
root.left = TreeNode(4)
root.right = TreeNode(10)
root.left.left = TreeNode(3)
root.left.right = TreeNode(5)
4

出力

10