データ構造における円のk-最短経路アルゴリズム

単一の最短経路を与える代わりに、Yenのk-最短経路アルゴリズムは kを与えます 2番目に短いパスと3番目に短いパスを取得できるようにするための最短パス。

場所Aから場所Bに移動する必要があり、場所Aと場所Bの間に複数のルートが利用可能であるというシナリオを考えてみましょう。ただし、最短パスを見つけて、その観点からあまり考慮されていないすべてのパスを無視する必要があります。目的地に到達するための時間計算量。

例を挙げて理解しましょう-

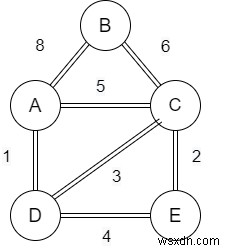
与えられた例をBのピークを持つ橋と考えてください。誰かがAからCに橋を渡りたい場合、誰も橋を渡るためにピークに行くことはありません。したがって、AからCへのパスは少し長くなります。

最短経路を取得する方法は複数あります。ただし、（k-1）までの最短経路を見つける必要があります。

k-最短経路のアルゴリズム

query= “””
MATCH(start: place{id:source}),*end: Place {Id:destination})
Call algo.kshortestPaths.stream(start,end,10, “distance”)
Yield nodeIDs, path costs, index
Return index.
   [node in algo.getNodeByID(nodeId[1…..-1]) | node.id] aS,
   Reduce (acc=0.0, cost in costs | acc+cost ) as total cost
“””
params= {“source”: Alex,Destination: “US”}
With driver.selection() as session:
  Row session.run(query, params)
  df = pd.DataFrame[dict(record) for record in rows])
pd.set_option(‘max_colwidth’, 100)
display(df)