データ構造のB+ツリー
ここでは、B+ツリーとは何かを確認します。 B +ツリーは、Bツリーの拡張バージョンです。このツリーは、Bツリーのより良い挿入、削除、および検索をサポートします。
Bツリー、キー、およびレコード値は、内部ノードとリーフノードに格納されます。 B +ツリーレコードでは、リーフノードに保存できます。内部ノードはキー値のみを保存します。 B+ツリーのリーフノードもリンクリストのようにリンクされています
B+ツリーの例 −
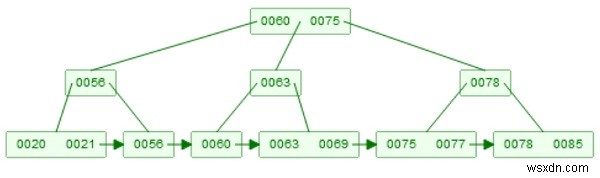
これは、検索、挿入、削除などの基本的な操作をサポートします。各ノードで、アイテムが並べ替えられます。位置iの要素には、その前後に子があります。したがって、以前に痛んだ子供は小さい値を保持し、右側にいる子供は大きい値を保持します。
Bツリーに対する利点
-
レコードは同数のディスクアクセスでフェッチできます
-
木の高さはバランスが取れており、Bツリーと比較して低くなっています
-
リーフはリンクリストのように接続されているため、要素を順番に検索することもできます
-
キーはインデックス作成に使用されます
-
データはリーフレベルでのみ保存されるため、検索が高速になります。
-
データ構造における二分木ADT
基本概念 二分木は、ノードが3つを超える子を持つことができないツリーとして定義されます。ノードの最高次数は2です。これは、二分木の次数が0または1または2であることを示しています。 上の図では、二分木はルートと2つのサブツリーTreeLeftとTreeRightで構成されています。二分木の左側にあるすべてのノードは左側のサブツリーと呼ばれ、二分木の右側にあるすべてのノードは右側のサブツリーと呼ばれます。 実装 二分木には最大2つの子があります。それらに直接ポインタを割り当てることができます。ツリーノードの宣言は、ノードがキー情報に加えて他のノードへの2つのポインタ(左と右)を含む構
-
データ構造の仮想ツリーでのスプレー
仮想ツリーでは、一部のエッジは実線として扱われ、一部は破線として扱われます。通常のスプレイは、堅い木でのみ実行されます。仮想ツリーのノードyで表示するには、次の方法を実装します。 アルゴリズムは、パスごとに1回ずつ、ツリーを3回調べ、それを変更します。最初のパスでは、ノードyから開始して、ソリッドツリーのみでスプレイすることにより、yからツリー全体のルートへのパスが破線になります。このパスは、スプライシングによって確実に作成されます。ノードyでの最後のスプレイにより、yがツリーのルートになります。非公式ではありませんが、アルゴリズムは次のように説明されています Splay(y)のアルゴリズ
