データ構造のk-aryツリー
このセクションでは、K-aryツリーとは何かを確認します。 K-aryツリーはルートツリーであり、各ノードは最大k個の子を保持できます。
kの値が2の場合、これは二分木と呼ばれます。二分木、または三分木は、いくつかの特殊なk-ary木です。したがって、k-aryツリーは一般化されます。
K-aryツリーの例 −
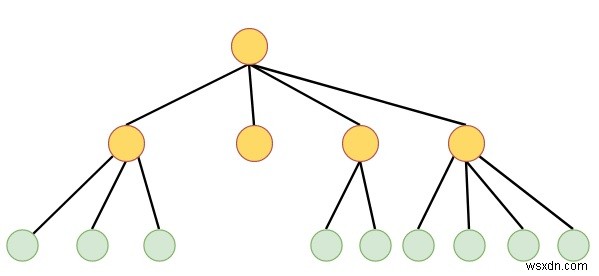
上記の例では、ルートがあります。ルートには4つの子があります。ルートの各子には、いくつかの子もあります。最初の子供には3人の子供がいて、2番目の子供には子供がなく、3番目の子供には2人の子供がいて、最後の子供には4人の子供がいます。
-
データ構造の範囲ツリー
範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O(log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k)が、O(n log d-1 のストレージが悪い n)、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ
-
データ構造の仮想ツリーでのスプレー
仮想ツリーでは、一部のエッジは実線として扱われ、一部は破線として扱われます。通常のスプレイは、堅い木でのみ実行されます。仮想ツリーのノードyで表示するには、次の方法を実装します。 アルゴリズムは、パスごとに1回ずつ、ツリーを3回調べ、それを変更します。最初のパスでは、ノードyから開始して、ソリッドツリーのみでスプレイすることにより、yからツリー全体のルートへのパスが破線になります。このパスは、スプライシングによって確実に作成されます。ノードyでの最後のスプレイにより、yがツリーのルートになります。非公式ではありませんが、アルゴリズムは次のように説明されています Splay(y)のアルゴリズ
