データ構造のセグメントツリー

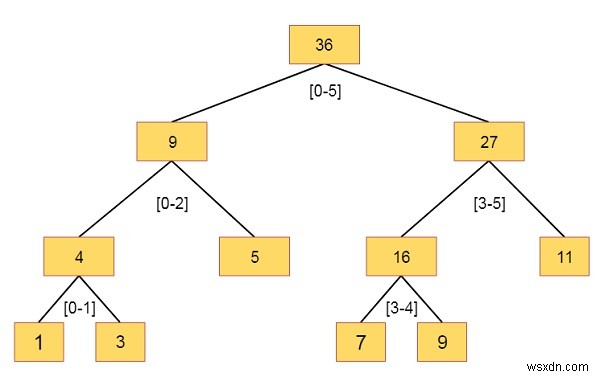
データ構造の範囲ツリー

範囲ツリーは、ポイントのリストを保持するための順序付けられたツリーデータ構造として定義されます。これにより、特定の範囲内のすべてのポイントを効率的に取得でき、通常は2次元以上で実装されます。 O（log d のクエリ時間が速いことを除いて、kdツリーと同じです。 n + k）が、O（n log d-1 のストレージが悪い n）、dはスペースの次元を示し、nはツリー内のポイントの数を示し、kは特定のクエリで取得されたポイントの数を示します。範囲ツリーは、間隔ツリーで区別できます。ポイントを格納して特定の範囲内のポイントを効率的に取得できるようにする代わりに、間隔ツリーは間隔を保存し、特定のポ

データ構造内の高さが制限されたハフマンツリー

高さ制限または深さ制限のハフマンツリーの図を以下に示します ツリーの深さの制限は、ほとんどの実際のハフマンの実装が対処しなければならない重要な問題です。 ハフマン構造は高さや深さを制限しません。もしそうなら、それが「最適」である可能性はありません。確かに、ハフマンツリーの最大の深さはフィボナッチ数列によって制限されますが、それは必要以上の深さのための十分な余地を残します。 ハフマンツリーの深さを制限する理由は何ですか？高速ハフマンデコーダーはルックアップテーブルを実装します。メモリコストを軽減するために複数のテーブルレベルを実装することは可能ですが、Huff0などの非常に高速なデコ