最小コストのポリゴン三角形分割
交差しない対角線が多角形で三角形を形成している場合、それは三角形分割と呼ばれます。私たちの仕事は、三角測量の最小コストを見つけることです。
三角測量のコストは、そのコンポーネントの三角形の重みの合計です。各三角形の重さは、辺を追加することでわかります。つまり、重さは三角形の周囲長です。
入力と出力
Input:
The points of a polygon. {(0, 0), (1, 0), (2, 1), (1, 2), (0, 2)}
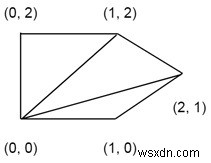 Output:
The total cost of the triangulation. Here the cost of the triangulation is 15.3006.
Output:
The total cost of the triangulation. Here the cost of the triangulation is 15.3006. アルゴリズム
minCost(polygon, n)
入力: ポリゴンを作成するための一連のポイントと、いくつかのポイント。
出力- ポリゴンの三角形分割の最小コスト。
Begin if n < 3, then return 0 define table or order n x n i := 0 for gap := 0 to n-1, do for j := gap to n-1, do if j < i+2, then table[i,j] := 0 else table[i, j] = ∞ for k := i+1 to j-1, do val := table[i, k] + table[k, j] + cost(i, j, k) if table[i, j] > val table[i, j] := val i := i + 1 done done return table[0, n-1] End
例
#include <iostream>
#include <cmath>
#include <iomanip>
#define MAX 1000000.0
using namespace std;
struct Point {
int x, y;
};
double min(double x, double y) {
return (x <= y)? x : y;
}
double dist(Point p1, Point p2) { //find distance from p1 to p2
return sqrt(pow((p1.x-p2.x),2) + pow((p1.y-p2.y),2));
}
double cost(Point triangle[], int i, int j, int k) {
Point p1 = triangle[i], p2 = triangle[j], p3 = triangle[k];
return dist(p1, p2) + dist(p2, p3) + dist(p3, p1); //the perimeter of the triangle
}
double minimumCost(Point polygon[], int n) {
if (n < 3) //when polygon has less than 3 points
return 0;
double table[n][n];
for (int gap = 0; gap < n; gap++) {
for (int i = 0, j = gap; j < n; i++, j++) {
if (j < i+2)
table[i][j] = 0.0;
else {
table[i][j] = MAX;
for (int k = i+1; k < j; k++) {
double val = table[i][k] + table[k][j] + cost(polygon,i,j,k);
if (table[i][j] > val)
table[i][j] = val; //update table data to minimum value
}
}
}
}
return table[0][n-1];
}
int main() {
Point points[] = {{0, 0}, {1, 0}, {2, 1}, {1, 2}, {0, 2}};
int n = 5;
cout <<"The minimumcost: " <<minimumCost(points, n);
} 出力
The minimumcost: 15.3006
-
Pythonですべてのポイントを接続するための最小コストを見つけるためのプログラム
(x、y)の形式のいくつかの点を持つpointsという配列があるとします。ここで、2つのポイント(xi、yi)と(xj、yj)を接続するコストは、それらの間のマンハッタン距離であり、式は| xi--xj|です。 + | yi--yj|。すべてのポイントを接続するための最小コストを見つける必要があります。 したがって、ここでの合計距離は(6 + 5 + 3 + 8)=22です。 これを解決するには、次の手順に従います- points_set:=範囲0からポイントのサイズ-1までの数値を保持する新しいセット ヒープ:=ペア(0、0)でヒープを作成します visited_node:
-
Pythonで最小コストで都市を接続する
1からNまでの番号が付けられたN個の都市があるとします。接続があります。各接続[i]は[city1、city2、cost]で、これはcity1とcity2を接続するためのコストを表します。 。都市のすべてのペアに対して、これら2つの都市を接続する接続パス(おそらく長さ1)が存在するように、最小コストを見つける必要があります。コストは、使用された接続コストの合計です。タスクが不可能な場合は、-1を返します。 したがって、グラフが次のような場合- その場合、出力は6になります。任意の2つの都市を選択すると、すべての都市が接続されるため、最小の2、[1、5]を選択します。 これを解決する
