2D行列の最大合計長方形

行列が与えられます。合計が最大になる長方形（場合によっては正方形）の行列を見つける必要があります。

このアルゴリズムの背後にある考え方は、左列と右列を修正し、各行の左列から右列までの要素の合計を見つけて、一時的に保存することです。一番上の行と一番下の行の番号を見つけようとします。一時配列を取得した後、Kadaneのアルゴリズムを適用して、最大合計サブ配列を取得できます。これにより、全体の長方形が形成されます。

入力と出力

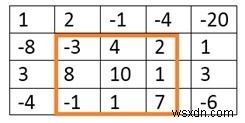
Input:
The matrix of integers.
 1  2 -1 -4 -20
-8 -3  4  2   1
 3  8  10 1   3
-4 -1   1 7  -6

Output:
The top left point and bottom right point of the submatrix, and the total sum of the submatrix.
(Top, Left) (1, 1)
(Bottom, Right) (3, 3)
The max sum is: 29

アルゴリズム

kadaneAlgorithm（array、start、end、n）

入力： 配列は、合計、開始点と終了点、要素の数を保持します。

出力- 開始点と終了点を見つけます。

Begin
   sum := 0 and maxSum := - ∞
   end := -1
   tempStart := 0

   for each element i in the array, do
      sum := sum + array[i]
      if sum < 0, then
         sum := 0
         tempStart := i + 1
      else if sum > maxSum, then
         maxSum := sum
         start := tempStart
         end := i
   done

   if end ≠ -1, then
      return maxSum
   maxSum := array[0], start := 0 and end := 0

   for each element i from 1 to n of array, do
      if array[i] > maxSum, then
         maxSum := array[i]
         start := i and end := i
   done

   return maxSum
End

maxSumRect（Matrix）

入力： 与えられた行列。

出力： 長方形の最大合計。

Begin
   maxSum := - ∞
   define temp array, whose size is same as row of matrix

   for left := 0 to number of columns in the Matrix, do
      till temp array with 0s
      for right := left to column of matrix -1, do
         for each row i, do
            temp[i] := matrix[i, right]
         done

         sum := kadaneAlgorithm(temp, start, end, number of rows)
            if sum > maxSum, then
               maxSum := sum
               endLeft := left
               endRight := right
               endTop := start
               endBottom := end
      done
   done

   display top left and bottom right corner and the maxSum
End

例

#include<iostream>
#define ROW 4
#define COL 5
using namespace std;

int M[ROW][COL] = {
   {1, 2, -1, -4, -20},
   {-8, -3, 4, 2, 1},
   {3, 8, 10, 1, 3},
   {-4, -1, 1, 7, -6}
 };

int kadaneAlgo(int arr[], int &start, int &end, int n) {    //find max sum and starting and ending location
   int sum = 0, maxSum = INT_MIN;

   end = -1;    //at first no place is selected

   int tempStart = 0;    //starting from 0

   for (int i = 0; i < n; i++) {
      sum += arr[i];
      if (sum < 0) {
         sum = 0;
         tempStart = i+1;
      }else if (sum > maxSum) {     //get maximum sum, and update start and end index
         maxSum = sum;
         start = tempStart;
         end = i;
      }
   }

   if (end != -1)
      return maxSum;
   //when all elements are negative in the array
   maxSum = arr[0];
   start = end = 0;

   // Find the maximum element in array
   for (int i = 1; i < n; i++) {
      if (arr[i] > maxSum) {
         maxSum = arr[i];
         start = end = i;
      }
   }
   return maxSum;
}

void maxSumRect() {
   int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;

   int left, right;
   int temp[ROW], sum, start, end;

   for (left = 0; left < COL; left++) {
      for(int i = 0; i<ROW; i++)//temp initially holds all 0
         temp[i] = 0;

      for (right = left; right < COL; ++right) {
         for (int i = 0; i < ROW; ++i)    //for each row, find the sum
            temp[i] += M[i][right];
         sum = kadaneAlgo(temp, start, end, ROW);    //find sum of rectangle (top, left) and (bottom right)

         if (sum > maxSum) {    //find maximum value of sum, then update corner points
            maxSum = sum;
            endLeft = left;
            endRight = right;
            endTop = start;
            endBottom = end;
         }
      }
   }

   cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
   cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
   cout << "The max sum is: "<< maxSum;
}

int main() {
   maxSumRect();
}

出力

(Top, Left) (1, 1)
(Bottom, Right) (3, 3)
The max sum is: 29

最小コストパス

最大合計増加部分列

Python –Kサイズのサブアレイの最大合計で行列を並べ替える
kサイズのサブアレイの最大合計で行列を並べ替える必要がある場合は、「amx」メソッドと「sum」メソッドを使用してリストを反復処理するメソッドが定義されます。例以下は同じもののデモンストレーションです def sort_marix_K(my_list): return max(sum(my_list[index: index + K]) for index in range(len(my_list) - K)) my_list = [[51, 23, 4, 24, 1], [45, 6, 26, 36, 5], [56, 16, 6, 36, 8], [5, 4, 36, 26,
Pythonで各行要素を反転して最大合計を見つけるプログラム
2Dバイナリ行列があるとします。指定された行列の任意の行または列について、すべてのビットを反転できます。これらの操作をいくつでも実行でき、各行を2進数として扱う場合は、これらの数値で作成できる最大の合計を見つける必要があります。したがって、入力が次のような場合 0 1 0 0 0 1 その場合、出力は11になり、両方の行を反転すると101と110が得られ、合計は5 + 6=11になりますこれを解決するには、次の手順に従います- 行列の各行rについて、次のようにします r [0]が0と同じ場合、 0からrのサイズの範囲のiについては、 r