指定された開始文字からの最長の連続パス

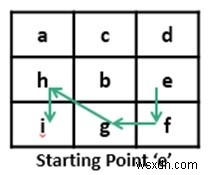
最長のパスを見つけるために、深さ優先探索アルゴリズムを使用します。 DFS中に、いくつかのサブ問題が複数回発生する場合があります。その計算を避けるために、何度も動的計画法を使用します。

入力と出力

Input:
The matrix as shown above. And the starting point. Here the starting point is e.
Output:
Enter Starting Point (a-i): e
Maximum consecutive path: 5

アルゴリズム

findLongestLen（i、j、prev）

入力： iとjおよび前の文字を配置します。

出力： 最長の長さ。

Begin
   if (i, j) place is valid or prev and matrix[i,j] are adjacent, then
      return 0
   if longestPath[i, j] is already filled, then
      return longestPath[i, j]
   len := 0

   for all its nearest 8 rooms k, do
      len := maximum of len and (1 + findLongestLen(i, x[k], j +y[k], matrix[i, j]))
   done

   longestPath[i, j] := len
   return len
End

getLen（start）

入力- 開始点。

出力- 最大長。

Begin
   for all row r of matrix, do
      for all column c, of matrix, do
         if matrix[i, j] = start, then
            for all adjacent room k, do
               len := maximum of len and (1 + findLongestLen(i, x[k], j +y[k], matrix[i, j])))
            done
      done
   done
   return len
End

例

#include<iostream>
#define ROW 3
#define COL 3
using namespace std;

// tool matrices to recur for adjacent cells.
int x[] = {0, 1, 1, -1, 1, 0, -1, -1};
int y[] = {1, 0, 1, 1, -1, -1, 0, -1};
int longestPath[ROW][COL];

char mat[ROW][COL] = {
   {'a','c','d'},
   {'h','b','a'},
   {'i','g','f'}
 };

int max(int a, int b) {
   return (a>b)?a:b;
}

bool isvalid(int i, int j) {
   if (i < 0 || j < 0 || i >= ROW || j >= COL)    //when i and j are in range
      return false;
   return true;
}

bool isadjacent(char previous, char current) {
   return ((current - previous) == 1);    //check current and previous are adjacent or not
}

int findLongestLen(int i, int j, char prev) {
   if (!isvalid(i, j) || !isadjacent(prev, mat[i][j]))    //when already included or not adjacent
      return 0;

   if (longestPath[i][j] != -1)
      return longestPath[i][j];     //subproblems are solved already

   int len = 0;  // Initialize result to 0

   for (int k=0; k<8; k++)    //find length of the largest path recursively
      len = max(len, 1 + findLongestLen(i + x[k], j + y[k], mat[i][j]));
   return longestPath[i][j] = len;    // save the length and return
}

int getLen(char start) {
   for(int i = 0; i<ROW; i++)
      for(int j = 0; j<COL; j++)
         longestPath[i][j] = -1;    //set all elements to -1

   int len = 0;

   for (int i=0; i<ROW; i++) {
      for (int j=0; j<COL; j++) {    // check for all possible starting point
         if (mat[i][j] == start)  {
            for (int k=0; k<8; k++)    //for all eight adjacent cells
               len = max(len, 1 + findLongestLen(i + x[k], j + y[k], start));
         }
      }
   }
   return len;
}

int main() {
   char start;
   cout << "Enter Starting Point (a-i): "; cin >> start;
   cout << "Maximum consecutive path: " << getLen(start);
   return 0;
}

出力

Enter Starting Point (a-i): e
Maximum consecutive path: 5