特定のグラフがツリーであるかどうかを確認します

この問題では、無向グラフが1つ与えられ、グラフがツリーであるかどうかを確認する必要があります。木の基準を確認するだけで簡単に見つけることができます。ツリーにはサイクルが含まれないため、グラフにサイクルがある場合、それはツリーではありません。

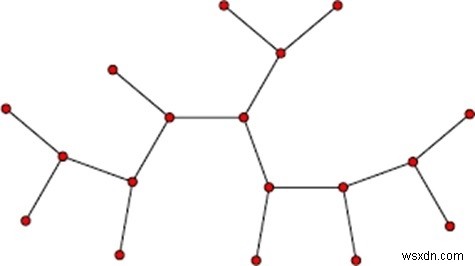
別のアプローチを使用して確認できます。グラフが接続されていて、V-1エッジがある場合は、ツリーである可能性があります。ここで、Vはグラフ内の頂点の数です。

入力と出力

Input:
The adjacency matrix.
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
1 1 1 1 0

Output:
The Graph is a tree

アルゴリズム

isCycle（u、visited、parent）

入力： 開始頂点u、訪問済みかどうかをマークする訪問済みリスト、親頂点。

出力： グラフにサイクルがある場合は真。

Begin
   mark u as visited
   for all vertex v which are adjacent with u, do
      if v is visited, then
         if isCycle(v, visited, u) = true, then
            return true
         else if v ≠ parent, then
            return true
   done
   return false
End

isTree（グラフ）

入力： 無向グラフ。

出力： グラフがツリーの場合はTrue。

Begin
   define a visited array to mark which node is visited or not
   initially mark all node as unvisited
   if isCycle(0, visited, φ) is true, then //the parent of starting vertex is null
      return false
   if the graph is not connected, then
      return false
   return true otherwise
End

例

#include<iostream>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 1, 1, 1, 0},
   {1, 0, 1, 0, 0},
   {1, 1, 0, 0, 0},
   {1, 0, 0, 0, 1},
   {0, 0, 0, 1, 0}
};
                                                               
bool isCycle(int u, bool visited[], int parent) {
   visited[u] = true;    //mark v as visited
   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {
         if(!visited[v]) {     //when the adjacent node v is not visited
            if(isCycle(v, visited, u)) {
               return true;
            }
         } else if(v != parent) {    //when adjacent vertex is visited but not parent
            return true;    //there is a cycle
         }
      }
   }
   return false;
}

bool isTree() {
   bool *vis = new bool[NODE];

   for(int i = 0; i<NODE; i++)
      vis[i] = false;    //initialize as no node is visited
         
   if(isCycle(0, vis, -1))    //check if there is a cycle or not
      return false;
         
   for(int i = 0; i<NODE; i++) {
      if(!vis[i])    //if there is a node, not visited by traversal, graph is not connected
         return false;
   }
   return true;
}

int main() {
   if(isTree())
      cout << "The Graph is a Tree.";
   else
      cout << "The Graph is not a Tree.";
}

出力

The Graph is a Tree.