有向グラフの接続性
グラフの接続性を確認するために、トラバーサルアルゴリズムを使用してすべてのノードをトラバースしようとします。トラバーサルの完了後、アクセスされていないノードがある場合、グラフは接続されていません。
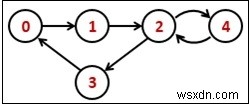
有向グラフの場合、接続を確認するためにすべてのノードからトラバースを開始します。 1つのエッジに外側のエッジのみがあり、内側のエッジがない場合があるため、ノードは他の開始ノードからアクセスされません。
この場合、トラバーサルアルゴリズムは再帰的なDFSトラバーサルです。
入力と出力
Input: Adjacency matrix of a graph 0 1 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 Output: The Graph is connected.
traverse(u、visited)
入力: 開始ノードuと訪問済みノードは、どのノードが訪問されたかをマークします。
出力- 接続されているすべての頂点をトラバースします。
Begin mark u as visited for all vertex v, if it is adjacent with u, do if v is not visited, then traverse(v, visited) done End
isConnected(graph)
入力: グラフ。
出力: グラフが接続されている場合はTrue。
Begin define visited array for all vertices u in the graph, do make all nodes unvisited traverse(u, visited) if any unvisited node is still remaining, then return false done return true End
例
#include<iostream>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0},
{0, 0, 1, 0, 0},
{0, 0, 0, 1, 1},
{1, 0, 0, 0, 0},
{0, 1, 0, 0, 0}
};
void traverse(int u, bool visited[]) {
visited[u] = true; //mark v as visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(!visited[v])
traverse(v, visited);
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i<NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i<NODE; i++) {
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
int main() {
if(isConnected())
cout << "The Graph is connected.";
else
cout << "The Graph is not connected.";
} 出力
The Graph is connected.
-
JavaFXシーングラフの説明
JavaFXでは、GUIアプリケーションはシーングラフを使用して構築されていました。シーングラフは、最新のグラフィカルアプリケーションにおけるツリーに似たデータ構造です。これはアプリケーションの開始点であり、ノードのコレクションです JavaFXで何かを表示するにはノードを使用してシーングラフを作成し、それをJavaFXアプリケーションの最上位コンテナであるStageクラスのオブジェクトに設定する必要があります。 ノードは、JavaFXアプリケーションの視覚的/グラフィカルなプリミティブオブジェクトです。 シーングラフの各ノードには単一の親があり、親を含まないノードはルートノードと呼
-
Pythonで有向グラフを反転するプログラム
有向グラフがあるとすると、その逆を見つける必要があるため、エッジがuからvに移動すると、vからuに移動します。ここで入力は隣接リストになり、ノードがn個ある場合、ノードは(0、1、...、n-1)になります。 したがって、入力が次のような場合 その場合、出力は次のようになります これを解決するには、次の手順に従います- ans:=n個の異なるリストのリスト。nは頂点の数です 各インデックスi、およびグラフ内の隣接リストlについて、実行します lのxごとに、 ans [x]の最後にiを挿入します 回答を返す 理解を深めるために、次の実装を見てみましょう- 例
