すべてのサイクルをC++の無向グラフに出力します

この問題では、無向グラフが与えられ、グラフに形成されるすべてのサイクルを印刷する必要があります。

無向グラフ 互いに接続されたグラフです。一方向グラフのすべてのエッジは双方向です。無向ネットワークとも呼ばれます。

サイクル グラフのデータ構造は、すべての頂点がサイクルを形成するグラフです。

問題をよりよく理解するための例を見てみましょう-

グラフ-

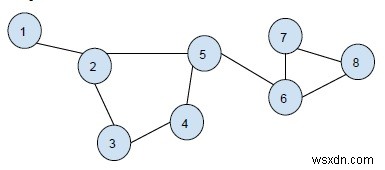
出力-

Cycle 1: 2 3 4 5
Cycle 2: 6 7 8

このために、グラフのいくつかのプロパティを利用します。グラフ彩色法を使用して、閉路グラフで発生するすべての頂点に色を付ける必要があります。また、頂点が部分的に訪問されると、閉路グラフが生成されます。したがって、同じ頂点に再び到達するまで、この頂点と次のすべての頂点に色を付けます。

アルゴリズム

Step 1: call DFS traversal for the graph which can color the vertices.
Step 2: If a partially visited vertex is found, backtrack till the vertex is
reached again and mark all vertices in the path with a counter which is cycle number.
Step 3: After completion of traversal, iterate for cyclic edge and push them
into a separate adjacency list.
Step 4: Print the cycles number wise from the adjacency list.

例

#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
vector<int> graph[N];
vector<int> cycles[N];
void DFSCycle(int u, int p, int color[], int mark[], int par[], int&amp; cyclenumber){
   if (color[u] == 2) {
      return;
   }
   if (color[u] == 1) {
      cyclenumber++;
      int cur = p;
      mark[cur] = cyclenumber;
      while (cur != u) {
         cur = par[cur];
         mark[cur] = cyclenumber;
      }
      return;
   }
   par[u] = p;
   color[u] = 1;
   for (int v : graph[u]) {
      if (v == par[u]) {
         continue;
      }
      DFSCycle(v, u, color, mark, par, cyclenumber);
   }
   color[u] = 2;
}
void insert(int u, int v){
   graph[u].push_back(v);
   graph[v].push_back(u);
}
void printCycles(int edges, int mark[], int&amp; cyclenumber){
   for (int i = 1; i <= edges; i++) {
      if (mark[i] != 0)
         cycles[mark[i]].push_back(i);
   }
   for (int i = 1; i <= cyclenumber; i++) {
      cout << "Cycle " << i << ": ";
      for (int x : cycles[i])
         cout << x << " ";
      cout << endl;
   }
}
int main(){
   insert(1, 2);
   insert(2, 3);
   insert(3, 4);
   insert(4, 5);
   insert(5, 2);
   insert(5, 6);
   insert(6, 7);
   insert(7, 8);
   insert(6, 8);
   int color[N];
   int par[N];
   int mark[N];
   int cyclenumber = 0;
   cout<<"Cycles in the Graph are :\n";
   int edges = 13;
   DFSCycle(1, 0, color, mark, par, cyclenumber);
   printCycles(edges, mark, cyclenumber);
}

出力

グラフのサイクルは-

Cycle 1: 2 3 4 5
Cycle 2: 6 7 8