C++の二分木で最大値の根を数える

したがって、入力が次のような場合

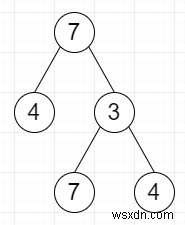
その場合、出力は3を除くすべてのノードとして4になり、基準を満たします。

これを解決するには、次の手順に従います-

• 関数dfs（）を定義します。これはノードを取ります

• ノードがnullでない場合、-

  • 0を返す

• l：=dfs（ノードの左側）

• r：=dfs（ノードの右側）

• ノードの値>=lとrの最大値の場合、-

  • （retを1増やします）

• x：=ノードのvalの最大値、lおよびr

• xを返す

• メインの方法から、次のようにします。

• ret：=0

• dfs（root）

• retを返す

理解を深めるために、次の実装を見てみましょう-

例

#include <bits/stdc++.h>
using namespace std;
class TreeNode {
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data) {
      val = data;
      left = NULL;
      right = NULL;
   }
};
class Solution {
   public:
   int ret;
   int dfs(TreeNode* node){
      if(!node)
         return 0;
      int l = dfs(node->left);
      int r = dfs(node->right);
      if(node->val >= max(l, r)) {
         ret++;
      }
      int x = max({node->val, l, r});
      return x;
   }
   int solve(TreeNode* root) {
      ret = 0;
      dfs(root);
      return ret;
   }
};
main(){
   Solution ob;
   TreeNode *root = new TreeNode(7);
   root->left = new TreeNode(4);
   root->right = new TreeNode(3);
   root->right->left = new TreeNode(7);
   root->right->right = new TreeNode(5);
   cout << (ob.solve(root));
}

入力

TreeNode *root = new TreeNode(7);
root->left = new TreeNode(4);
root->right = new TreeNode(3);
root->right->left = new TreeNode(7);
root->right->right = new TreeNode(5);

出力

4