データ構造におけるB+ツリーの削除

ここでは、B+ツリーからノードを削除する方法を説明します。 7マイナス以下のようなB+ツリーがあるとします;

B+ツリーの例 −

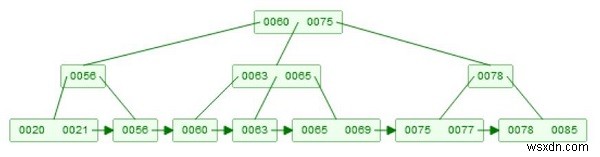
削除には2つの部分があります。まず、要素を見つける必要があります。その戦略はクエリのようなものです。ここで削除するには、いくつかのルールに注意する必要があります。 1つのノードには少なくともm/2個の要素が必要です。したがって、1つの要素を削除し、残りの要素がm-1未満の場合、それ自体が調整されます。ノード全体が削除されると、その子がマージされ、それらのサイズがmと同じである場合、それらを2つの部分に分割すると、中央値が再び上がります。

78を削除するとします。これで2人の子がいます。 [75、77]、および[78、85]の場合、最初にリーフノードから78を削除し、その後85を取得して、キー85のコピーを作成し、サブツリーのルートとして作成します。

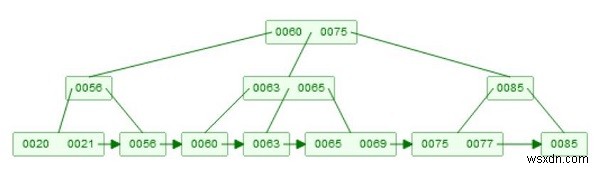
アルゴリズム

BPlusTreeDelete（x、key） −

入力-ツリーのルート、および削除するキー

We will assume, that the key is present into the list
Start from root node, perform exact match for key as ‘key’ till a leaf node. Let the search path
be x1, x2, … , xh. The x1 is first node so root, then xh is leaf node. Each node xi is parent of xi+1
delete the object where key is ‘key’ from xh.
if h = 1, then return, as there is only one node which is root.
i := h
while xi underflows, do
   if immediate sibling node s of xi, has at least m/2 + 1 elements, then
      redistribute entries evenly between s and xi.
      corresponding to redistribution, a key k in the parent node xi-1, will be changed.
      if xi is non-leaf node, then
         k is dragged down to xi. and a key from s is pushed up to fill the place of k
      else
         k is simply replaced by a key in s
      return
   else
      merge xi with the sibling node s. Delete the corresponding child pointer in xi-1.
      if xi is an internal node, then
         drag the key in xi-1. which is previously divides xi and s. into the new node
         xi and s, into the new node xi.
      else
         delete that key in xi-1.
      i := i – 1
   end if
done