プログラミング
 Computer >> コンピューター >  >> プログラミング >> プログラミング

データ構造のオイラーグラフとハミルトングラフ

このセクションでは、オイラーグラフとハミルトングラフを表示します。しかし、それに飛び込む前に、最初にグラフの軌跡が何であるかを確認する必要があります。以下のようなグラフが1つあるとします-

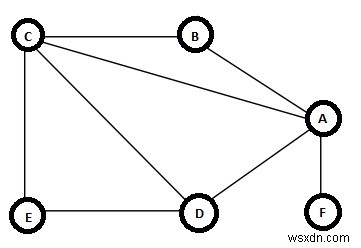
データ構造のオイラーグラフとハミルトングラフ

トレイルはパスであり、エッジ（v1、v2）、（v2、v3）、…、（vk-1、vk）のシーケンスであり、すべての頂点（v1、v2、…、vk）が区別されない場合があります。 、ただし、すべてのエッジが異なります。この例では、1つのトレイルは{（B、A）、（A、C）、（C、D）、（D、A）、（A、F）}です。これはトレイルです。ただし、頂点Aが2回アクセスされるため、これは単純なパスとは見なされません。最初と最後の頂点が同じである場合、それは閉じたトレイルになります。

オイラートレイル

グラフG（V、E）のオイラートレイルは、すべてのエッジを1回だけ含むトレイルです。 Gがオイラートレイルを閉じた場合、そのグラフはオイラーグラフと呼ばれます。言い換えれば、グラフGはオイラーグラフであると言えます。1つの頂点から開始する場合、すべてのエッジを1回だけトラバースして、開始頂点に戻ることができます。オイラーは、すべての頂点の次数が偶数である場合にのみ、グラフがオイラーグラフと呼ばれることを証明しました。

ハミルトンサイクル

1つのサイクルがグラフGのすべての頂点を通過する場合、ハミルトン閉路と呼ばれます。グラフがハミルトンになるための十分条件を与える多くの異なる定理があります。ただし、任意のグラフがハミルトニアンであるかどうかを判断する問題は、NPComplete問題です。


  1. データ構造における適応型マージとソート

    アダプティブマージソート アダプティブマージソートは、ソートされたサブリストのマージソートを実行します。ただし、最初のサブリストのサイズは、サイズ1のサブリストではなく、要素のリスト間の順序の存在に依存します。たとえば、図のリストについて考えてみます。 2つのソートされたサブリストで構成されています。 要素16、15、14、13を含むサブリスト1。 要素9、10、11、12のサブリスト2。 サブリスト1はソートされていますが、逆の順序になっています。したがって、サブリスト1は、図に示すように逆になります。 サブリストが見つかると、マージプロセスが

  2. グラフとその走査アルゴリズム

    このセクションでは、グラフデータ構造とそのトラバーサルアルゴリズムについて説明します。 グラフは1つの非線形データ構造です。これは、いくつかのノードとそれらの接続されたエッジで構成されています。エッジは、ディレクターまたは無向の場合があります。このグラフは、G（V、E）として表すことができます。次のグラフは、G（{A、B、C、D、E}、{（A、B）、（B、D）、（D、E）、（B、C）、（C、A ）}） グラフには、2種類のトラバーサルアルゴリズムがあります。これらは、幅優先探索および深さ優先探索と呼ばれます。 幅優先探索（BFS） 幅優先探索（BFS）トラバーサルはアルゴリズムであ