プログラミング
 Computer >> コンピューター >  >> プログラミング >> プログラミング

データ構造の有向グラフの深さ優先探索

グラフの深さ優先探索も同様です。しかし、有向グラフまたは有向グラフの場合、いくつかのタイプのエッジを見つけることができます。 DFSアルゴリズムは、DFSツリーと呼ばれるツリーを形成します。 -

と呼ばれるエッジには4つのタイプがあります

  • ツリーエッジ（T） −DFSツリーに存在するエッジ

  • フォワードエッジ（F） −ツリーエッジのセットに平行。 （小さいDFS番号から大きいDFS番号へ、大きいDFS完了番号から小さいDFS完了番号へ）

  • バックワードエッジ（B） −大きいDFS番号から小さいDFS番号へ、小さいDFS完了番号から大きいDFS完了番号へ。

  • クロスエッジ（C） −大きいDFS番号から小さいDFS番号、大きいDFS完了番号から小さいDFS完了番号。

以下のようなグラフがあるとします-

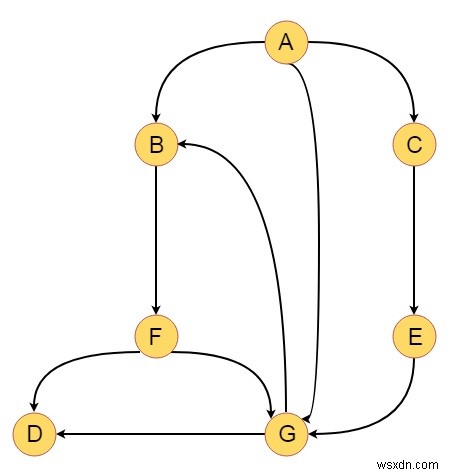
データ構造の有向グラフの深さ優先探索

次に、Aを初期頂点としてDFSを実行し、DFS番号とDFS完了番号を入力します。したがって、ツリーは次のようになります-

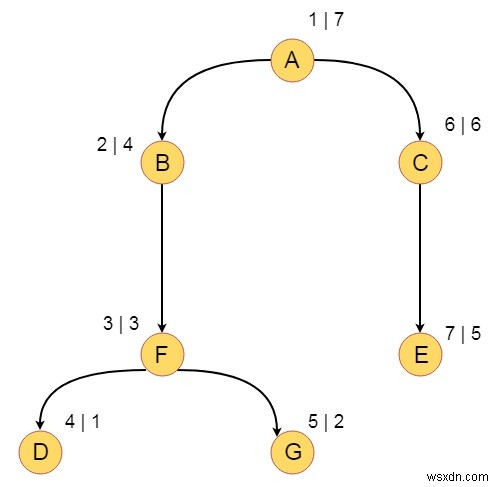
データ構造の有向グラフの深さ優先探索

つまり、DFSトラバーサルはA、B、F、D、G、C、Eです

ツリーのエッジは− T ={（A、B）、（B、F）、（F、D）、（F、G）、（A、C）、（C、E）}

前方エッジは− F ={（A、G）}

後方エッジは− B ={（G、B）}

クロスエッジは-C={（G、D）}

です。
  1. データ構造の線形プロービング

    このセクションでは、オープンアドレッシングスキームでの線形プロービング手法とは何かを説明します。通常のハッシュ関数h´（x）：U→{0、1、。 。 。、m –1}。オープンアドレッシングスキームでは、実際のハッシュ関数h（x）は通常のハッシュ関数h’（x）を取り、それに別の部分を付加して1つの線形方程式を作成します。 h´（𝑥）=𝑥𝑚𝑜𝑑𝑚 ℎ（𝑥、𝑖）=（ℎ´（𝑥）+𝑖）𝑚𝑜𝑑𝑚 i|の値=0、1 、。 。 。、m – 1.したがって、i =0から開始し、1つの空き領域が得られるまでこれを増やします。したがって、最初にi =0の場合、h（x、i）はh´（x）

  2. ハーフエッジデータ構造

    はじめに テンプレートパラメータまたはハーフエッジデータ構造（HalfedgeDSと略記）のHDSは、平面マップ、多面体、またはその他の方向付け可能な2次元など、頂点、エッジ、および面の入射情報を維持できるエッジ中心のデータ構造として定義されます。ランダムな次元に埋め込まれたサーフェス。各エッジは、反対方向の2つのハーフエッジに分割されます。各ハーフエッジには、1つの入射面と1つの入射頂点が格納されます。各面と各頂点に1つの入射ハーフエッジが格納されます。ハーフエッジデータ構造のバリエーションを減らすと、面のハーフエッジポインタや面の保存など、この情報の一部を削除できます。 ハーフエッジデ