償却分析
この分析は、時折の操作が非常に遅い場合に使用されますが、非常に頻繁に実行される操作のほとんどは高速です。ハッシュテーブル、互いに素なセットなどの償却分析が必要なデータ構造
ハッシュテーブルでは、ほとんどの場合、検索時間の複雑さはO(1)ですが、O(n)操作を実行することもあります。ほとんどの場合、ハッシュテーブルで要素を検索または挿入する場合、タスクは一定時間かかりますが、衝突が発生すると、衝突を解決するためにO(n)回の操作が必要になります。
集計方法
総コストを見つけるために集計方法が使用されます。大量のデータを追加する場合は、この式で償却原価を見つける必要があります。
n回の操作のシーケンスの場合、コストは-
です。

償却分析の例
動的配列の場合、アイテムはO(1)時間で特定のインデックスに挿入できます。ただし、そのインデックスが配列に存在しない場合、一定時間でタスクを実行できません。その場合、最初に配列のサイズを2倍にし、インデックスが存在する場合は要素を挿入します。
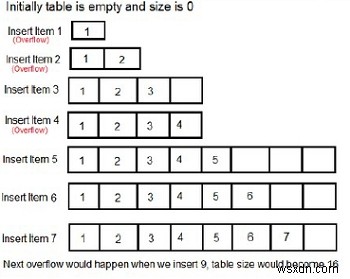
動的配列の場合、let = ithのコスト 挿入。
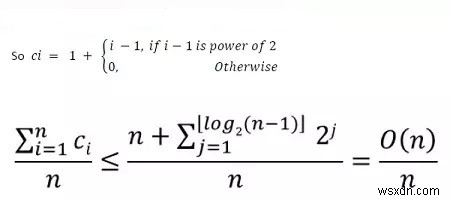
-
データ構造の償却時間計算量
償却分析 この分析は、時折の操作が非常に遅い場合に使用されますが、非常に頻繁に実行される操作のほとんどは高速です。データ構造では、ハッシュテーブル、互いに素なセットなどの償却分析が必要です。 ハッシュテーブルでは、ほとんどの場合、検索時間の複雑さはO(1)ですが、O(n)操作を実行することもあります。ほとんどの場合、ハッシュテーブルで要素を検索または挿入する場合、タスクは一定時間かかりますが、衝突が発生すると、衝突を解決するためにO(n)回の操作が必要になります。 集計方法 総コストを見つけるために集計方法が使用されます。大量のデータを追加する場合は、この式で償却原価を見つける必要があり
-
Pythonでのベクトル化
この記事では、Python3.xを使用した実装に関連するベクトル化とさまざまな手法について学習します。またはそれ以前。 ベクトル化とは何ですか? ベクトル化は、ループを使用せずに配列を実装する手法です。代わりに関数を使用すると、コードの実行時間と実行時間を効率的に最小化するのに役立ちます。さまざまな演算が、ベクトルの内積などの配列ではなく、ベクトルに対して実行されています。これは、単一の出力を生成するため、スカラー積とも呼ばれます。外部積は、ベクトルの(長さXの長さ)に等しい次元の二乗行列になります。要素同じインデックスの要素と行列の次元を積む賢明な乗算は変更されません。 内積/内積
