漸近表記
漸近表記は、漸近分析のアルゴリズムの複雑さを表すために使用されます。これらの表記は、複雑さを表す数学的ツールです。一般的に使用される表記法は3つあります。
ビッグオー表記
Big-Oh(O)表記は、関数f(n)の上限を定数係数内に与えます。
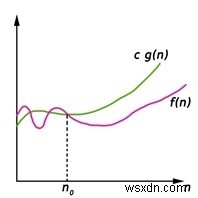
f(n)=O(g(n))と書くと、正の定数n0とcがあり、n0の右側で、f(n)は常にc * g(n)以下になります。
>O(g(n))={f(n):すべてのn≥n0に対して、0≤f(n)≤cg(n)となる正の定数cおよびn0が存在します}
ビッグオメガ表記
ビッグオメガ(Ω)表記は、関数f(n)の下限を一定の係数内に与えます。
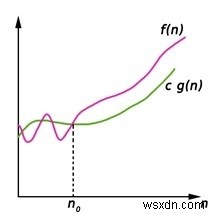
f(n)=Ω(g(n))と書く。正の定数n0とcがあり、n0の右側にある場合、f(n)は常にc * g(n)以上になります。
>Ω(g(n))={f(n):すべてのn≥n0に対して、0≤cg(n)≤f(n)となる正の定数cおよびn0が存在します}
ビッグシータ表記
Big-Theta(Θ)表記は、関数f(n)の限界を一定の係数内に与えます。
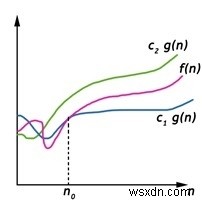
f(n)=Θ(g(n))と書く。正の定数n0とc1およびc2があり、n0の右側で、f(n)が常にc1 * g(n)とc2*gの間にある場合。 (n)包括的。
Θ(g(n))={f(n):すべてのn≥n0に対して、0≤c1g(n)≤f(n)≤c2g(n)となる正の定数c1、c2、およびn0が存在します}
-
漸近解析
漸近解析 漸近解析を使用すると、入力サイズに基づいてアルゴリズムのパフォーマンスについてのアイデアを得ることができます。正確な実行時間を計算する必要はありませんが、実行時間と入力サイズの関係を見つける必要があります。入力のサイズが大きくなるときは、実行時間を追跡する必要があります。 スペースの複雑さについては、アルゴリズムを完了するためにメインメモリ内のどのくらいのスペースが占有されているかという関係または関数を取得することが目標です。 漸近的振る舞い 関数の場合f(n) 漸近的な振る舞いは、nが大きくなるにつれてf(n)が大きくなることです。小さい入力値は考慮されません。私たちの仕事は
-
漸近的な複雑さ
漸近解析 漸近解析を使用すると、入力サイズに基づいてアルゴリズムのパフォーマンスについてのアイデアを得ることができます。正確な実行時間を計算する必要はありませんが、実行時間と入力サイズの関係を見つける必要があります。入力のサイズが大きくなるときは、実行時間を追跡する必要があります。 スペースの複雑さについては、アルゴリズムを完了するためにメインメモリ内のどのくらいのスペースが占有されているかという関係または関数を取得することが目標です。 漸近的振る舞い 関数の場合f(n) 漸近的な振る舞いは、nが大きくなるにつれてf(n)が大きくなることです。小さい入力値は考慮されません。私たちの仕事は
