データ構造の償却時間計算量
償却分析
この分析は、時折の操作が非常に遅い場合に使用されますが、非常に頻繁に実行される操作のほとんどは高速です。データ構造では、ハッシュテーブル、互いに素なセットなどの償却分析が必要です。
ハッシュテーブルでは、ほとんどの場合、検索時間の複雑さはO(1)ですが、O(n)操作を実行することもあります。ほとんどの場合、ハッシュテーブルで要素を検索または挿入する場合、タスクは一定時間かかりますが、衝突が発生すると、衝突を解決するためにO(n)回の操作が必要になります。
集計方法
総コストを見つけるために集計方法が使用されます。大量のデータを追加する場合は、この式で償却原価を見つける必要があります。
n回の操作のシーケンスの場合、コストは-
です。$ \ frac {Cost(n \:operations)} {n} =\ frac {Cost(normal \:operations)+ Cost(Expensive \:operations)} {n} $
償却分析の例
動的配列の場合、アイテムはO(1)時間で特定のインデックスに挿入できます。ただし、そのインデックスが配列に存在しない場合、一定時間でタスクを実行できません。その場合、最初に配列のサイズを2倍にし、インデックスが存在する場合は要素を挿入します。
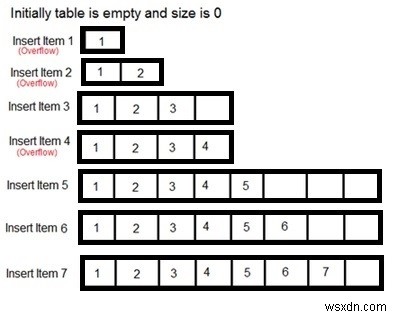
動的配列の場合、ci=i番目の挿入のコストとします。
$ So \:ci =1 + \ begin {cases} i \:-\:1、if \:i-1 \:is \:power \:of \:2 \\ 0、\:\:\:\ :\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:さもないと\ end {cases} $
$$ \ frac {\ displaystyle \ sum \ Limits_ {i =1} ^ n ci} {n} \ leq \ frac {n + \ displaystyle \ sum \ Limits_ {j =1} ^ {\ lfloor \ log {2} { \ lgroup n-1 \ rgroup} \ rfloor} 2j} {n} =\ frac {O \ lgroup n \ rgroup} {n} $$
-
漸近的な複雑さ
漸近解析 漸近解析を使用すると、入力サイズに基づいてアルゴリズムのパフォーマンスについてのアイデアを得ることができます。正確な実行時間を計算する必要はありませんが、実行時間と入力サイズの関係を見つける必要があります。入力のサイズが大きくなるときは、実行時間を追跡する必要があります。 スペースの複雑さについては、アルゴリズムを完了するためにメインメモリ内のどのくらいのスペースが占有されているかという関係または関数を取得することが目標です。 漸近的振る舞い 関数の場合f(n) 漸近的な振る舞いは、nが大きくなるにつれてf(n)が大きくなることです。小さい入力値は考慮されません。私たちの仕事は
-
通信ベースのデータ構造
トータルとリーフの対応は、より洗練された対応手法です。これらの手法の両方で、要素の半分は最小PQに配置され、残りの半分は最大PQに配置されます。要素数が奇数の場合、1つの要素がバッファに格納されます。このバッファリングされた要素は、どちらのPQのメンバーでもありません。トータルコレスポンデンス手法では、最小PQの各要素xは、最大PQの個別の要素yとペアになります。 (x、y)は、priority(x)<=priority(y)。のような対応する要素のペアです。 図Eは、11個の要素3、4、5、5、6、6、7、8、9、10、11の合計対応ヒープを示しています。要素10はバッファー内にあります。
