ツェラーのアルゴリズムを使用して平日を見つける

ツェラーのアルゴリズムは、特定の日付から平日を見つけるために使用されます。ツェラーのアルゴリズムを使用して平日を見つける式は次のとおりです。

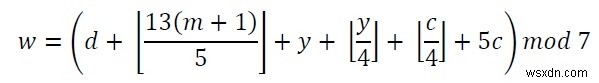
式にはいくつかの変数が含まれています。彼らは-

d −日付の日。

m：月コードです。 3月から12月までは3から12、1月は13、2月は14です。1月または2月を考慮すると、指定された年は1減少します。

y −年の最後の2桁

c −年の最初の2桁

w −平日。 0の場合は土曜日、6の場合は金曜日を意味します

入力と出力

Input:
The day, month and the year: 4, 1, 1997
Output:
It was: Saturday

アルゴリズム

zellersAlgorithm(day, month, year)

入力： その日の日付。

出力： どちらの日でしたか（日曜日から土曜日）。

Begin
   if month > 2, then
      mon := month
   else
      mon := 12 + month
      decrease year by 1
   y := last two digit of the year
   c := first two digit of the year
   w := day + floor((13*(mon+1))/5) + y + floor(y/4) + floor(c/4) + 5*c
   w := w mod 7
   return weekday[w] //weekday will hold days from Saturday to Friday
End

例

#include<iostream>
#include<cmath>
using namespace std;

string weekday[7] = {"Saturday","Sunday","Monday","Tuesday","Wednesday","Thursday","Friday"};
                               
string zellersAlgorithm(int day, int month, int year) {
   int mon;
   if(month > 2)
      mon = month;    //for march to december month code is same as month
   else {
      mon = (12+month);    //for Jan and Feb, month code will be 13 and 14
      year--; //decrease year for month Jan and Feb
   }
         
   int y = year % 100;    //last two digit
   int c = year / 100;    //first two digit
   int w = (day + floor((13*(mon+1))/5) + y + floor(y/4) + floor(c/4) + (5*c));
   w = w % 7;
   return weekday[w];
}

int main() {
   int day, month, year;
   cout << "Enter Day: "; cin >>day;
   cout << "Enter Month: "; cin >>month;
   cout << "Enter Year: "; cin >>year;
   cout << "It was: " <<zellersAlgorithm(day, month, year);
}

出力

Enter Day: 04
Enter Month: 01
Enter Year: 1997
It was: Saturday