2つの数を掛ける最速の方法

2つの数値は2進文字列として指定されます。私たちのタスクは、これらの数値の乗算の結果をより高速かつ効率的に見つけることです。

分割統治法を使用すると、非常に効率的な方法で問題を解決できます。数字を2つに分割します。

XleftとXrightが最初の数Xの2つの部分であり、Yleft、Yrightが2番目の数Yの2つの部分であるとします。したがって、製品;

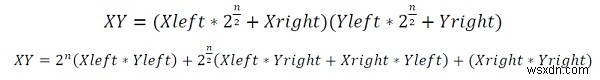
簡単にするために、この操作を実行できます

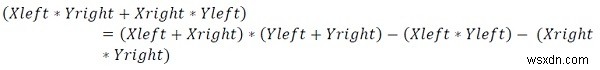
入力と出力

Input:
Two binary numbers: 1101 and 0111
Output:
The result is: 91

アルゴリズム

addBitString（num1、num2）

入力： 追加する2つの数字。

出力： 追加後の結果。

Begin
   adjust num1 and num2 lengths
   length := length of num1
   carry := 0

   for i := length -1 down to 0, do
      num1Bit := num1[i]
      num2Bit := num2[i]
      sum := num1Bit XOR num2Bit XOR carry
      finalSum := sum + finalSum
      carry := (num1Bit AND num2Bit) OR (num2Bit AND carry) OR (num1Bit AND carry)
   done

   if carry ≠ 0, then
      finalSum := 1 + finalSum
   return finalSum
End

multiply（num1、num2）

入力： 掛ける2つの数字。

出力： 乗算後の結果。

Begin
   adjust num1 and num2 lengths
   length := length of num1
   if n = 0, then
      return 0
   if n = 1, then
      return (num1[0] * num2[0])
   firstHalf := n/2
   secondHalf := (n - firstHalf)

   n1Left := substring of (0 to firstHalf) from num1
   n1Right := substring of (firstHalf to secondHalf) from num1
   n2Left := substring of (0 to firstHalf) from num2
   n2Right := substring of (firstHalf to secondHalf) from num2

   p1 := multiply(n1Left, n2Left)
   p2 := multiply(n1Right, n2Right)

   add1 := addBitString(n1Left, n1Right)
   add2 := addBitString(n2Left, n2Right)
   p3 := multiply(add1, add2)

   mask1 := shift 1 to left for 2*secondHalf bits
   mask2 := shift 1 to left for secondHalf bits
   return P1*mask2 + (p3 – p1 – p2)*mask2 + p2
End

例

#include<iostream>
using namespace std;

int lengthAdjust(string &num1, string &num2) {    //adjust length of binary string and send length of string
   int len1 = num1.size();
   int len2 = num2.size();

   if (len1 < len2) {
      for (int i = 0 ; i < len2 - len1 ; i++)
         num1 = '0' + num1; //add 0 before the first string
   } else if (len1 > len2) {
      for (int i = 0 ; i < len1 - len2 ; i++)
         num2 = '0' + num2; //add 0 before the second string
   }
   return num1.size();
}

string addBitStrings(string num1, string num2) {
   string finalSum;

   int length = lengthAdjust(num1, num2);    //adjust and update number lengths and store length
   int carry = 0;     // Initialize carry

   for (int i = length-1 ; i >= 0 ; i--) {
      int num1Bit = num1[i] - '0';
      int num2Bit = num2[i] - '0';

      int sum = (num1Bit ^ num2Bit ^ carry)+'0';    //we know sum = A XOR B XOR C

      finalSum = (char)sum + finalSum;
      //the carry = (A AND B) OR (B AND C) OR (C AND A)
      carry = (num1Bit&num2Bit) | (num2Bit&carry) | (num1Bit&carry);
   }

   if (carry)   //when carry is present
      finalSum = '1' + finalSum; //add carry as MSb
   return finalSum;
}

long int multiply(string num1, string num2) {
   int n = lengthAdjust(num1, num2);    //find length after adjusting them
   if (n == 0)    //when there is 0 length string, return 0
      return 0;
   if (n == 1)
      return (num1[0] - '0')*(num2[0] - '0');    //perform single bit muliplication

   int firstHalf = n/2;   // First half range
   int secondHalf = (n-firstHalf);    // Second half range

   string num1Left = num1.substr(0, firstHalf);    //first half of number 1
   string num1Right = num1.substr(firstHalf, secondHalf);    //second half of number 1
   string num2Left = num2.substr(0, firstHalf);
   string num2Right = num2.substr(firstHalf, secondHalf);

   // find left right multiplication, and multiply after adding left and right part
   long int P1 = multiply(num1Left, num2Left);
   long int P2 = multiply(num1Right, num2Right);
   long int P3 = multiply(addBitStrings(num1Left, num1Right), addBitStrings(num2Left, num2Right));

   return P1*(1<<(2*secondHalf)) + (P3 - P1 - P2)*(1<<secondHalf) + P2;
}

int main() {
   string num1, num2;
   cout << "Enter First number in Binary: "; cin >>num1;
   cout << "Enter Second number in Binary: "; cin >>num2;
   cout << "The result is: " << multiply(num1, num2);
}

出力

Enter First number in Binary: 1101
Enter Second number in Binary: 0111
The result is: 91