線形回帰

与えられたデータポイントのセットから、線形回帰は直線の方程式を見つけます。与えられたポイントは直線に従います。この式を使用して、現在セットに存在しない他の特定のポイントの値がどうなるかを予測できます。

いくつかのデータポイントを使用して線形回帰の問題を解決するには、次の式に従う必要があります。

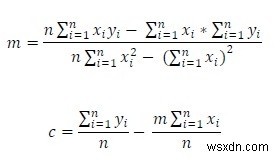
ここで、mとcはそれぞれ傾きとy切片です。これらの式を使用すると、次の形式で直線の方程式を得ることができます。𝑦=𝑚𝑥+𝑐。

入力と出力

Input:
The (x, y) coordinates of some points. {(1,3), (2,4), (3,5), (4,6), (5,8)}
Output:
The slope: 1.2 The Intercept: 1.6
The equation: y = 1.2x + 1.6

アルゴリズム

linReg(coord)

入力： 与えられた座標点のセット。

出力： 傾きmとy切片c。

Begin
   for i := 1 to n, do
      sumX := sumX + coord[i,0]
      sumY := sumY + coord[i,1]
      sumXsq := sumXsq + (coord[i,0]*coord[i,0])
      sumXY := sumXY + (coord[i,0] * coord[i,1])
   done

   m := (n * sumXY – (sumX*sumY)) / (n * sumXsq – (sumX * sumX))
   c := (sumY / n) – (m * sumX)/n
End

例

#include<iostream>
#include<cmath>
#define N 5
using namespace std;

void linReg(int coord[N][2], float &m, float &c) {
   float sx2 = 0, sx = 0, sxy = 0, sy = 0;
   for(int i = 0; i<N; i++) {
      sx += coord[i][0];    //sum of x
      sy += coord[i][1];   //sum of y

      sx2 += coord[i][0]*coord[i][0];      //sum of x^2
      sxy += coord[i][0]*coord[i][1];     //sum of x*y
   }

   // finding slope and intercept
   m = (N*sxy-(sx*sy))/(N*sx2-(sx*sx));
   c = (sy/N)-(m*sx)/N;
}

main() {
   // this 2d array holds coordinate points
   int point[N][2] = {{1,3},{2,4},{3,5},{4,6},{5,8}};
   float m, c;
   linReg(point, m, c);
   cout << "The slope: " << m << " The Intercept: " << c << endl;
   cout << "The equation: " << "y = "<< m <<"x + "<< c;
}

出力

The slope: 1.2 The Intercept: 1.6
The equation: y = 1.2x + 1.6