目的地に到達するための最小初期ポイント

特定のグリッドの左上隅から開始するには、右下隅に到達する必要があります。グリッド内の各セルには数値が含まれ、数値は正または負の場合があります。人がセル（i、j）に到達すると、そのセルの値に応じて、持っているトークンの数が増減する場合があります。旅を完了するために必要な初期トークンの最小数を見つける必要があります。

いくつかのルールがあります-

• 右または下に移動できます。
• 合計トークンが（i、j）の値よりも小さい場合、セル（i、j）に移動することはできません。
• プラスのポイントを最小限に抑えて目的地に到達する必要があります。

入力と出力

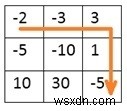
Input:
The token for each room as a matrix.
-2  -3  3
-5 -10  1
10  30 -5

Output:
The minimum token required to start the journey. For this example, the required token is 7.

アルゴリズム

minInitTokens(matrix)

入力： 各部屋のトークンマトリックス。

出力- 出発地から目的地まで到達するために必要な最小トークン。

Begin
   define matrix minToken of size same as matrix
   m := number of rows in matrix
   n := number of columns in matrix

   if matrix[m-1, n-1] > 0, then
      minToken[m-1, n-1] := 0
   else
      minToken[m-1, n-1] := 1 + absolute value of matrix[m-1, n-1]

   for i := m-2 down to 0, do
      minToken[i, n-1] := maximum of 1 and (minToken[i+1, n-1]-matrix[i,n-1])
   done

   for j := n-2 down to 0, do
      minToken[m-1, j] := maximum of 1 and (minToken[m-1, j+1]-matrix[m-1, j])
   done

   for i := m-2 down to 0, do
      for j := n-2 down to 0, do
         rem := minimum of minToken[i+1, j] and minToken[i, j+1]
         minPoint[i, j] := maximum of 1 and (rem – matrix[i,j])
      done
   done

   return minToken[0, 0]
End

例

#include<iostream>
#include<cmath>
#define ROW 3
#define COL 3
using namespace std;

int tokens[ROW][COL] = {
   {-2,-3,3},
   {-5,-10,1},
   {10,30,-5}
};

int max(int a, int b) {
   return (a>b)?a:b;
}

int minInitPoints() {
   int minToken[ROW][COL];
   int m = ROW, n = COL;
   
   minToken[m-1][n-1] = tokens[m-1][n-1] > 0? 1: abs(tokens[m-1][n-1]) + 1;
   
   for (int i = m-2; i >= 0; i--)    //from last row to first row, fill points
      minToken[i][n-1] = max(minToken[i+1][n-1] - tokens[i][n-1], 1);
   
   for (int j = n-2; j >= 0; j--)    //fill last column to first column, fill points
      minToken[m-1][j] = max(minToken[m-1][j+1] - tokens[m-1][j], 1);

   for (int i=m-2; i>=0; i--) {
      for (int j=n-2; j>=0; j--) {
         int remPoint = min(minToken[i+1][j], minToken[i][j+1]);    //calculate remaining points
         minToken[i][j] = max(remPoint - tokens[i][j], 1);
      }
   }
   return minToken[0][0];
}

int main() {
   cout << "Minimum Points Required: " << minInitPoints();
}

出力

Minimum Points Required: 7