有向非巡回グラフの最長パス

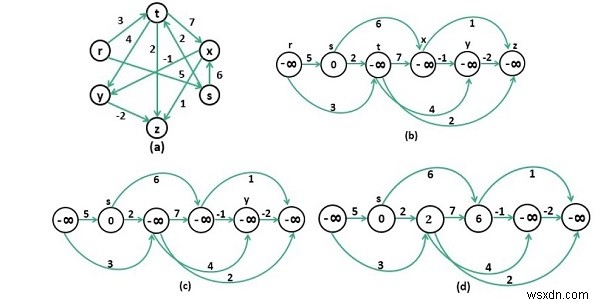
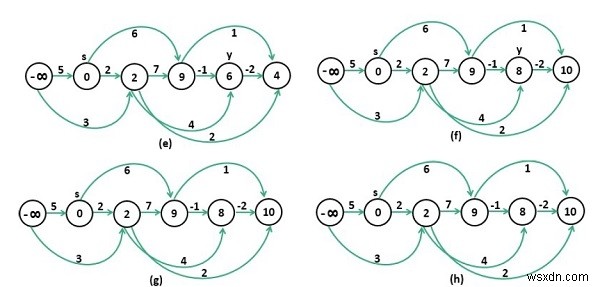
トポロジカルソート手法でノードをソートする必要があり、トポロジカルソート後の結果はスタックに格納されます。その後、スタックから繰り返しポップし、各頂点の最長距離を見つけようとします。

入力と出力

Input:
The cost matrix of the graph.
0  5   3 -∞ -∞ -∞
-∞ 0   2  6 -∞ -∞
-∞ -∞  0  7  4  2
-∞ -∞ -∞  0 -1  1
-∞ -∞ -∞ -∞  0 -2
-∞ -∞ -∞ -∞ -∞  0

Output:
Longest Distance from Source Vertex 1
Infinity 0 2 9 8 10

アルゴリズム

topoSort（u、visited、stack）

入力： 開始ノードu、追跡するために訪問したリスト、スタック。

出力- トポロジ的な方法でノードを並べ替えます。

Begin
   mark u as visited
   for all vertex v, which is connected with u, do
      if v is not visited, then
         topoSort(v, visited, stack)
   done
   push u into the stack
End

longestPath（start）

入力- 開始ノード。

出力- 開始ノードからのすべての頂点の最長距離のリスト。

Begin
   initially make all nodes as unvisited
   for each node i, in the graph, do
      if i is not visited, then
         topoSort(i, visited, stack)
   done

   make distance of all vertices as - ∞
   dist[start] := 0
   while stack is not empty, do
      pop stack item and take into nextVert
      if dist[nextVert] ≠ - ∞, then
         for each vertices v, which is adjacent with nextVert, do
            if cost[nextVert, v] ≠ - ∞, then
               if dist[v] < dist[nectVert] + cost[nextVert, v], then
                  dist[v] := dist[nectVert] + cost[nextVert, v]
         done
   done

   for all vertices i in the graph, do
      if dist[i] = - ∞, then
         display Infinity
      else
         display dist[i]
   done
End

例

#include<iostream>
#include<stack>
#define NODE 6
#define INF -9999
using namespace std;

int cost[NODE][NODE] = {
   {0, 5, 3, INF, INF, INF},
   {INF, 0, 2, 6, INF, INF},
   {INF, INF, 0, 7, 4, 2},
   {INF, INF, INF, 0, -1, 1},
   {INF, INF, INF, INF, 0, -2},
   {INF, INF, INF, INF, INF, 0}
};

void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;    //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(cost[u][v]) {    //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }

   stk.push(u);    //push starting vertex into the stack
}

void longestPath(int start) {
   stack<int> stk;
   int dist[NODE];
   bool vis[NODE];

   for(int i = 0; i<NODE;i++)
      vis[i] = false;    // make all nodes as unvisited at first
         
   for(int i = 0; i<NODE; i++)    //perform topological sort for vertices
      if(!vis[i])
         topoSort(i, vis, stk);
               
   for(int i = 0; i<NODE; i++)
      dist[i] = INF;    //initially all distances are infinity
   dist[start] = 0;    //distance for start vertex is 0
   
   while(!stk.empty()) {    //when stack contains element, process in topological order
      int nextVert = stk.top(); stk.pop();

      if(dist[nextVert] != INF) {
         for(int v = 0; v<NODE; v++) {
            if(cost[nextVert][v] && cost[nextVert][v] != INF) {
               if(dist[v] < dist[nextVert] + cost[nextVert][v])
                  dist[v] = dist[nextVert] + cost[nextVert][v];
            }
         }
      }
   }
     
   for(int i = 0; i<NODE; i++)
      (dist[i] == INF)?cout << "Infinity ":cout << dist[i]<<" ";
}

main() {
   int start = 1;
   cout << "Longest Distance From Source Vertex "<<start<<endl;
   longestPath(start);
}

出力

Longest Distance From Source Vertex 1
Infinity 0 2 9 8 10