有向グラフのオイラー回路

オイラーパスは、すべてのエッジを1回だけ訪問できるパスです。同じ頂点を複数回使用できます。オイラー回路は、特殊なタイプのオイラーパスです。オイラーパスの開始頂点がそのパスの終了頂点にも接続されている場合、それはオイラー回路と呼ばれます。

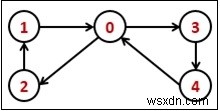
グラフがオイラーであるかどうかを確認するには、2つの条件を確認する必要があります-

• グラフを接続する必要があります。
• 各頂点の次数と次数は同じである必要があります。

入力と出力

Input:
Adjacency matrix of the graph.
0 1 0 0 0
0 0 1 0 0
0 0 0 1 1
1 0 0 0 0
0 0 1 0 0

Output:
Euler Circuit Found.

アルゴリズム

traverse（u、visited）

入力： 開始ノードuと訪問済みノードは、どのノードが訪問されたかをマークします。

出力： 接続されているすべての頂点をトラバースします。

Begin
   mark u as visited
   for all vertex v, if it is adjacent with u, do
      if v is not visited, then
         traverse(v, visited)
   done
End

isConnected（グラフ）

入力- グラフ。

出力- グラフが接続されている場合はTrue。

Begin
   define visited array
   for all vertices u in the graph, do
      make all nodes unvisited
      traverse(u, visited)
      if any unvisited node is still remaining, then
         return false
   done
   return true
End

isEulerCircuit（グラフ）

入力： 与えられたグラフ。

出力： オイラー回路が1つ見つかった場合は真です。

Begin
   if isConnected() is false, then
      return false
   define list for inward and outward edge count for each node

   for all vertex i in the graph, do
      sum := 0
      for all vertex j which are connected with i, do
         inward edges for vertex i increased
         increase sum
      done
      number of outward of vertex i is sum
   done

   if inward list and outward list are same, then
      return true
   otherwise return false
End

例

#include<iostream>
#include<vector>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 1, 0, 0, 0},
   {0, 0, 1, 0, 0},
   {0, 0, 0, 1, 1},
   {1, 0, 0, 0, 0},
   {0, 0, 1, 0, 0}
};
               
void traverse(int u, bool visited[]) {
   visited[u] = true;    //mark v as visited

   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {
         if(!visited[v])
            traverse(v, visited);
      }
   }
}

bool isConnected() {
   bool *vis = new bool[NODE];
   //for all vertex u as start point, check whether all nodes are visible or not

   for(int u; u < NODE; u++) {
      for(int i = 0; i<NODE; i++)
         vis[i] = false;    //initialize as no node is visited
               
      traverse(u, vis);
         
      for(int i = 0; i<NODE; i++) {
         if(!vis[i])    //if there is a node, not visited by traversal, graph is not connected
            return false;
      }
   }
   return true;
}

bool isEulerCircuit() {
   if(isConnected() == false) {    //when graph is not connected
      return false;
   }

   vector<int> inward(NODE, 0), outward(NODE, 0);
         
   for(int i = 0; i<NODE; i++) {
      int sum = 0;
      for(int j = 0; j<NODE; j++) {
         if(graph[i][j]) {
            inward[j]++;    //increase inward edge for destination vertex
            sum++;    //how many outward edge
         }
      }
      outward[i] = sum;
   }

   if(inward == outward)    //when number inward edges and outward edges for each node is same
      return true;
   return false;
}

int main() {
   if(isEulerCircuit())
      cout << "Euler Circuit Found.";
   else
      cout << "There is no Euler Circuit.";
}

出力

Euler Circuit Found.