二重連結グラフ

2つの頂点の間に2つの頂点が互いに素なパスが存在する場合、無向グラフは2重連結グラフと呼ばれます。つまり、任意の2つの頂点の間にサイクルがあると言えます。

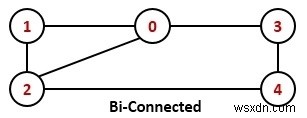
グラフGは、接続されていて、グラフに関節点や切断点が存在しない場合、2重連結グラフであると言えます。

この問題を解決するために、DFSトラバーサルを使用します。 DFSを使用して、アーティキュレーションポイントが存在するかどうかを確認します。また、すべての頂点がDFSによってアクセスされているかどうかを確認します。アクセスされていない場合は、グラフが接続されていないと言えます。

入力と出力

Input:
The adjacency matrix of the graph.
0 1 1 1 0
1 0 1 0 0
1 1 0 0 1
1 0 0 0 1
0 0 1 1 0

Output:
The Graph is a biconnected graph.

アルゴリズム

isArticulation （開始、訪問済み、ディスク、低、親）

入力： 開始頂点、ノードが訪問されたときにマークする訪問済み配列、ディスクは頂点の検出時間を保持し、lowはサブツリーに関する情報を保持します。親は現在の頂点の親を保持します。

出力- アーティキュレーションポイントが見つかった場合はTrue。

Begin
   time := 0      //the value of time will not be initialized for next function calls
   dfsChild := 0
   mark start as visited
   set disc[start] := time+1 and low[start] := time + 1
   time := time + 1

   for all vertex v in the graph G, do
      if there is an edge between (start, v), then
         if v is visited, then
            increase dfsChild
            parent[v] := start

            if isArticulation(v, visited, disc, low, parent) is true, then
               return ture
            low[start] := minimum of low[start] and low[v]

            if parent[start] is φ AND dfsChild > 1, then
               return true

            if parent[start] is φ AND low[v] >= disc[start], then
               return true
         else if v is not the parent of start, then
            low[start] := minimum of low[start] and disc[v]
   done
   return false
End

isBiconnected（グラフ）

入力： 与えられたグラフ。

出力- グラフが2重連結の場合はTrue。

Begin
   initially set all vertices are unvisited and parent of each vertices are φ
   if isArticulation(0, visited, disc, low, parent) = true, then
      return false

   for each node i of the graph, do
      if i is not visited, then
         return false
   done
   return true
End

例

#include<iostream>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 1, 1, 1, 0},
   {1, 0, 1, 0, 0},
   {1, 1, 0, 0, 0},
   {1, 0, 0, 0, 1},
   {0, 0, 0, 1, 0}
};
                               
int min(int a, int b) {
   return (a<b)?a:b;
}
                               
bool isArticulation(int start, bool visited[], int disc[], int low[], int parent[]) {
   static int time = 0;
   int dfsChild = 0;
   visited[start] = true;    //make the first vertex is visited
   disc[start] = low[start] = ++time;    //initialize discovery time and the low time

   for(int v = 0; v<NODE; v++) {
      if(graph[start][v]) {   //for all vertex v, which is connected with start
         if(!visited[v]) {
            dfsChild++;
            parent[v] = start;    //make start node as parent
            if(isArticulation(v, visited, disc, low, parent))
               return true;
            low[start] = min(low[start], low[v]);    //when subtree from v is connected to one of parent of start node
            if(parent[start] == -1 && dfsChild > 1) {    //when u have 2 or more children
               return true;
            }

            if(parent[start] != -1 && low[v]>= disc[start])
               return true;
         } else if(v != parent[start])    //update low of start for previous call
            low[start] = min(low[start], disc[v]);
      }
   }
   return false;
}

bool isBiConnected() {
   bool *vis = new bool[NODE];
   int *disc = new int[NODE];
   int *low = new int[NODE];
   int *parent = new int[NODE];
   
   for(int i = 0; i<NODE; i++) {
      vis[i] = false;    //no node is visited
      parent[i] = -1;    //initially there is no parent for any node
   }
   
   if(isArticulation(0, vis, disc, low, parent))    //when no articulation point is found
      return false;
   for(int i = 0; i<NODE; i++)
      if(!vis[i])    //if any node is unvisited, the graph is not connected
         return false;
   return true;
}

int main() {
   if(isBiConnected())
      cout << "The Graph is a biconnected graph.";
   else
      cout << "The Graph is not a biconnected graph.";
}

出力

The Graph is a biconnected graph.