クラスカルの最小スパニングツリーアルゴリズム

連結グラフG（V、E）があり、すべてのエッジの重みまたはコストが示されています。クラスカルのアルゴリズムは、グラフとコストを使用して最小全域木を見つけます。

これは、マージツリーアプローチです。最初はさまざまなツリーがありますが、このアルゴリズムは、コストが最小のエッジを取得することでそれらをマージし、単一のツリーを形成します。

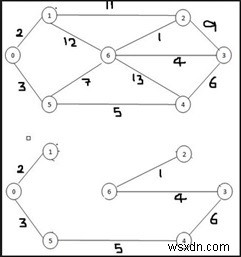
この問題では、すべてのエッジがリストされ、コストに基づいて並べ替えられます。リストから、最小コストのエッジが取り出されてツリーに追加され、エッジ形成サイクルかどうかがチェックされます。サイクルを形成する場合は、リストからエッジを破棄して次のエッジに進みます。

このアルゴリズムの時間計算量は、O（E log E）またはO（E log V）です。ここで、Eはエッジの数であり、Vは頂点の数です。

入力と出力

Input:
Adjacency matrix

Output:
Edge: B--A And Cost: 1
Edge: E--B And Cost: 2
Edge: F--E And Cost: 2
Edge: C--A And Cost: 3
Edge: G--F And Cost: 3
Edge: D--A And Cost: 4
Total Cost: 15

アルゴリズム

kruskal(g: Graph, t: Tree)

入力- 与えられたグラフgと空の木t

出力- 選択されたエッジを持つツリーt

Begin
   create set for each vertices in graph g
   for each set of vertex u do
      add u in the vertexSet[u]
   done

   sort the edge list.
   count := 0
   while count <= V – 1 do    //as tree must have V – 1 edges
      ed := edgeList[count]   //take an edge from edge list
      if the starting vertex and ending vertex of ed are in same set then
         merge vertexSet[start] and vertexSet[end]
         add the ed into tree t
      count := count +1
   done
End

例

#include<iostream>
#define V 7
#define INF 999
using namespace std;

//Cost matrix of the graph
int costMat[V][V] = {
   {0, 1, 3, 4, INF, 5, INF},
   {1, 0, INF, 7, 2, INF, INF},
   {3, INF, 0, INF, 8, INF, INF},
   {4, 7, INF, 0, INF, INF, INF},
   {INF, 2, 8, INF, 0, 2, 4},
   {5, INF, INF, INF, 2, 0, 3},
   {INF, INF, INF, INF, 4, 3, 0}
};

typedef struct {
   int u, v, cost;
}edge;

void swapping(edge &e1, edge &e2) {
   edge temp;
   temp = e1;
   e1 = e2;
   e2 = temp;
}

class Tree {
   int n;
   edge edges[V-1];    //as a tree has vertex-1 edges
   public:
      Tree() {
         n = 0;
      }

      void addEdge(edge e) {
         edges[n] = e;   //add edge e into the tree
         n++;
      }

      void printEdges() {    //print edge, cost and total cost
         int tCost = 0;

         for(int i = 0; i<n; i++) {
            cout << "Edge: " << char(edges[i].u+'A') << "--" <<char(edges[i].v+'A');
            cout << " And Cost: " << edges[i].cost << endl;
            tCost += edges[i].cost;
         }
         cout << "Total Cost: " << tCost << endl;
      }
};

class VSet {
   int n;
   int set[V];    //a set can hold maximum V vertices
   public:
      VSet() {
         n = -1;
      }

      void addVertex(int vert) {
         set[++n] = vert;    //add vertex to the set
      }

      int deleteVertex() {
         return set[n--];
      }

      friend int findVertex(VSet *vertSetArr, int vert);
      friend void merge(VSet &set1, VSet &set2);
};

void merge(VSet &set1, VSet &set2) {
   //merge two vertex sets together
   while(set2.n >= 0)
      set1.addVertex(set2.deleteVertex());
      //addToSet(vSet1, delFromSet(vSet2));
}

int findVertex(VSet *vertSetArr, int vert) {
   //find the vertex in different vertex sets
   for(int i = 0; i<V; i++)
      for(int j = 0; j<=vertSetArr[i].n; j++)
         if(vert == vertSetArr[i].set[j])
            return i;   //node found in i-th vertex set
}

int findEdge(edge *edgeList) {
   //find the edges from the cost matrix of Graph and store to edgeList
   int count = -1, i, j;
   for(i = 0; i<V; i++)
      for(j = 0; j<i; j++)
         if(costMat[i][j] != INF) {
            count++;
            //fill edge list for the position 'count'
            edgeList[count].u = i; edgeList[count].v = j;
            edgeList[count].cost = costMat[i][j];
         }
   return count+1;
}

void sortEdge(edge *edgeList, int n) {
   //sort the edges of graph in ascending order of cost
   int flag = 1, i, j;

   for(i = 0; i<(n-1) && flag; i++) {   //modified bubble sort is used
      flag = 0;
      for(j = 0; j<(n-i-1); j++)
         if(edgeList[j].cost > edgeList[j+1].cost) {
            swapping(edgeList[j], edgeList[j+1]);
            flag = 1;
         }
   }
}

void kruskal(Tree &tr) {
   int ecount, maxEdge = V*(V-1)/2;   //max n(n-1)/2 edges can have in a graph
   edge edgeList[maxEdge], ed;
   int uloc, vloc;
   VSet VSetArray[V];
   ecount = findEdge(edgeList);

   for(int i = 0; i < V; i++)
      VSetArray[i].addVertex(i);    //each set contains one element
   sortEdge(edgeList, ecount);      //ecount number of edges in the graph
   int count = 0;

   while(count <= V-1) {
      ed = edgeList[count];
      uloc = findVertex(VSetArray, ed.u);
      vloc = findVertex(VSetArray, ed.v);

      if(uloc != vloc) {    //check whether source abd dest is in same set or not
         merge(VSetArray[uloc], VSetArray[vloc]);
         tr.addEdge(ed);
      }
      count++;
   }
}

int main() {
   Tree tr;
   kruskal(tr);
   tr.printEdges();
}

出力

Edge: B--A And Cost: 1
Edge: E--B And Cost: 2
Edge: F--E And Cost: 2
Edge: C--A And Cost: 3
Edge: G--F And Cost: 3
Edge: D--A And Cost: 4
Total Cost: 15