無向グラフにC++で指定されたサイズの独立集合が含まれているかどうかを確認します

コンセプト

与えられた無向グラフに関して、サイズlの独立集合が含まれているかどうかを確認します。サイズlの独立集合が存在する場合は「はい」と印刷し、そうでない場合は「いいえ」と印刷します。グラフの独立集合は、互いに直接接続されていない頂点の集合として定義されることに注意してください。

入力

L = 4,
graph = [[1, 0, 1, 0, 0],
[0, 1, 1, 0, 0],[1, 1, 1, 1, 1],
[0, 0, 1, 1, 0],[0, 0, 1, 0, 1]];

出力

Yes

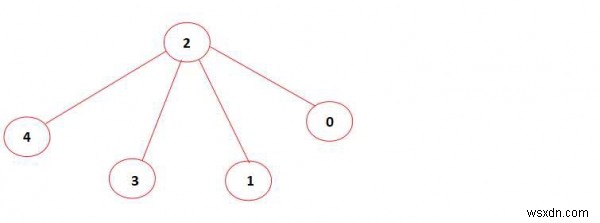
上のグラフには、サイズ4の独立したセットが含まれています（頂点0、1、3、4は互いに直接接続されていません）。したがって、出力は「はい」です。

入力

L = 4,
graph =[[1, 1, 1, 0, 0],[1, 1, 1, 0, 0],[1, 1, 1, 1, 1],[0, 0, 1, 1, 0],[0, 0, 1, 0, 1]];

出力

No

この図では、上のグラフにはサイズ4の独立したセットが含まれていません。したがって、出力は「いいえ」です。

メソッド

• 最初に、ブール値のFalse値を使用して変数solを初期化します。
• 指定されたグラフから、サイズLの可能なすべての頂点のセットを決定します。
• サイズlの独立したセットが見つかった場合は、solの値をTrueに変更して戻ります。
• それ以外の場合は、他の可能なセットのチェックを続けます。
• 最後に、solがTrueの場合は「はい」を印刷し、そうでない場合は「いいえ」を印刷します。

例

// C++ code to check if a given graph
// contains an independent set of size k
#include <bits/stdc++.h>
using namespace std;
// Shows function prototype
bool check1(int[][5], vector<int>&, int);
// Shows function to construct a set of given size l
bool func(int graph1[][5], vector<int>&arr1,
int l, int index1, bool sol1[]){
   // Verify if the selected set is independent or not.
   // Used to change the value of sol to True and return
   // if it is independent
      if (l == 0){
         if (check1(graph1, arr1, arr1.size())){
            sol1[0] = true;
            return true;
         }
      }
      else{
         // Now set of size l can be formed even if we don't
         // include the vertex at current index.
         if (index1 >= l){
            vector<int> newvec(arr1.begin(), arr1.end());
            newvec.push_back(index1);
            return (func(graph1, newvec, l - 1,
            index1 - 1, sol1) or
            func(graph1, arr1, l, index1 - 1, sol1));
         }
            // Now set of size l cannot be formed if we don't
         // include the vertex at current index.
         else{
            arr1.push_back(index1);
            return func(graph1, arr1, l - 1,
            index1 - 1, sol1);
         }
      }
   }
   // Shows function to verify if the given set is
   // independent or not
   // arr --> set of size l (contains the
   // index of included vertex)
   bool check1(int graph1[][5], vector<int>&arr1, int n1){
      // Verify if each vertex is connected to any other
         // vertex in the set or not
      for (int i = 0; i < n1; i++)
         for (int j = i + 1; j < n1; j++)
            if (graph1[arr1[i]][arr1[j]] == 1)
            return false;
      return true;
}
// Driver Code
int main(){
   int graph1[][5] = {{1, 0, 1, 0, 0},{0, 1, 1, 0, 0},{1, 1, 1, 1, 1},{0, 0, 1, 1, 0},
      {0, 0, 1, 0, 1}};
      int l = 4;
      vector<int> arr1; // Empty set
      bool sol1[] = {false};
      int n1 = sizeof(graph1) /
      sizeof(graph1[0]);
      func(graph1, arr1, l, n1 - 1, sol1);
      if (sol1[0])
         cout << "Yes" << endl;
      else
         cout << "No" << endl;
      return 0;
}

出力

Yes