C++で下から右に光を転送できる最大ミラー

0と1のみを含む正方行列が与えられます。 0は空白または空の場所を表し、1は障害物を意味します。これらのミラーが下から右に光を転送できるように、空のセルに配置できるミラーをいくつか見つける必要があります。これは、ミラーがインデックス[i、j]に配置され、その特定の行（i）の右側のすべてのセルと、その特定の列の下部（j）のセルに障害物がない場合に可能です。

ミラーがA[i][j]にある場合、すべてのA [i+1からn][j]およびA[i][j + 1からn]は空、つまり0です。次の図に示すように。

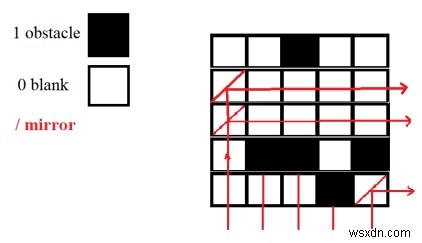
入力

Arr[][] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}}

出力

No. of mirrors : 3

説明 −図のように。ミラーはセルに配置できます

Arr [1] [0]-行1と列0には、その下と右にすべて0があります。

Arr [2] [0] −行2と列0には、その下と右にすべて0があります。

Arr [4] [4]-最後のセルは0で、下に行がなく、右に列があります。

以下のプログラムで使用されているアプローチは次のとおりです

• 配列Arr[][]は、0と1の行列を表すために使用されます。

• 関数maximumMirror（int mat [] []、int n）は行列を取り、その辺nを入力として受け取り、上記のように配置できる最大ミラーの数を返します。

• 可変フラグは、arr[i][j]の下のセルまたは右側のセルに障害物が存在することを示すために使用されます。

• カウントは、ミラーの数を表すために使用されます。最初は0です。

• インデックス0,0から行列をトラバースします。

• セルが空の場合（ミラーを配置できる場合）、下のセルを確認します（k =i + 1からn-1）。arr[k] [j]が障害物（値=1）の場合は、ループしてフラグを1としてマークします。そうでない場合は、右側のセルのチェックを続行します（l =j + 1からn-1）。

• 障害物が存在する場合に備えてフラグを設定します。

• 両方のwhileループの後、フラグが0の場合、ミラーを配置できるため、カウントをインクリメントします。

• いいえとしてカウントを返します。最大のミラーの数。

例

// C++ program to find how many mirrors can transfer
// light from bottom to right
#include <bits/stdc++.h>
using namespace std;
// method returns number of mirror which can transfer
// light from bottom to right
int maximumMirror(int mat[5][5], int N){
   // to mark that all cells in the right or bottom are 0---no obstacle
   int flag=0;
   int count=0; //count of mirrors
   int i,j,k,l;
   //for all cells
   for (int i=0; i<N; i++)
      for(j=0;j<N;j++){
   //check from next column and next row
   int k=i+1;
   int l=j+1;
   if(mat[i][j]==0) //position for mirror{
      while(k<N) //check for rows below{
         if(mat[k][j]==1) //keeping column fixed, if there is obstacle break{
            flag=0; break; }
      else
         flag=1;
         k++;
      }
      if(flag==1) //if no obstacle in rows then check columns in right
         while(l<N) //checking for columns in right{
            if(mat[i][l]==1) //keep row fixed, if obstacle break{
               flag=0; break;
         }
         else
            flag=1;
            l++;
         }
         if(flag==1) //there is no obstacle for mirror mat[i][j]
            count++;
      }
   }
   return count;
}
int main(){
   int N = 5;
   //matrix where 1 represents obstacle form 5X5 matrix
   int mat[5][5] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}};
   cout <<"Maximum mirrors which can transfer light from bottom to right :"<<
   maximumMirror(mat, N) << endl;
   return 0;
}

出力

Maximum mirrors which can transfer light from bottom to right :3