C++でのリスのシミュレーション

木、リス、そしていくつかのナッツがあります。位置は、2Dグリッドのセルで表されます。あなたの目標は、リスがすべてのナッツを集めて、それらを1つずつ木の下に置くための最小距離を見つけることです。リスは一度に最大で1つのナットしかとることができず、隣接するセルに向かって上下左右の4つの方向に移動できます。距離は移動回数で表されます。

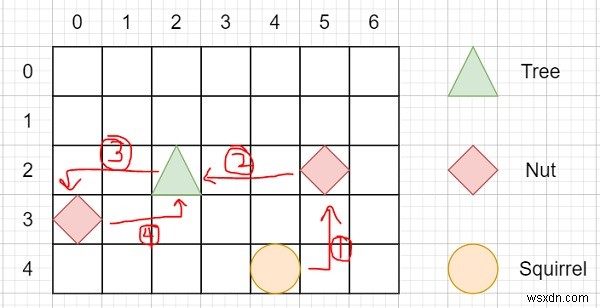
したがって、入力が高さ：5幅：7木の位置：[2,2]リス：[4,4]ナッツ：[[3,0]、[2,5]]の場合、出力は12になります。 、

これを解決するには、次の手順に従います-

• 関数calc（）を定義します。これには、x1、y1、x2、y2、

  が必要です。

• 戻り値|x1-x2| + | y1-y2 |

• 関数minDistance（）を定義します。これには、高さ、幅、配列ツリー、配列sq、2D配列ナット1つが必要です。

• ret：=0

• maxDiff：=-inf

• 初期化i：=0の場合、i <ナットのサイズの場合、更新（iを1増やします）、実行-

  • dist：=calc（tree [0]、tree [1]、nuts [i、0]、nuts [i、1]）

  • ret：=ret + 2 * dist

  • maxDiff：=maxDiffと2* distの最大値-（dist + calc（nuts [i、0]、nuts [i、1]、sq [0]、sq [1]））

• return ret --maxDiff

例

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int calc(int x1, int y1, int x2, int y2){
      return abs(x1 - x2) + abs(y1 - y2);
   }
   int minDistance(int height, int width, vector<int>& tree, vector<int>& sq, vector<vector>& nuts) {
      int ret = 0;
      int maxDiff = INT_MIN;
      for (int i = 0; i < nuts.size(); i++) {
         int dist = calc(tree[0], tree[1], nuts[i][0],
         nuts[i][1]);
         ret += 2 * dist;
         maxDiff = max(maxDiff, 2 * dist - (dist + calc(nuts[i][0], nuts[i][1], sq[0], sq[1])));
      }
      return ret - maxDiff;
   }
};
main(){
   Solution ob;
   vector<int> v = {2,2}, v1 = {4,4};
   vector<vector<int>> v2 = {{3,0}, {2,5}};
   cout << (ob.minDistance(5,7,v, v1, v2));
}

入力

5, 7, {2,2},{4,4}, {{3,0}, {2,5}}

出力

12